* intro
🍻 분할(Divide)하고 정복(Conquer)하는 알고리즘은 분할 → 정복 → 결합 크게 세 단계로 진행
🍻
① 분할(Divide): 주어진 문제를 더 작은 여러 개의 sub-problem으로 분할한다.
② 정복(Conquer): 재귀적으로 sub-problem들을 각각 해결한다. 문제들을 각각 독립적으로 해결.
③ 결합(Combine): 각각의 sub-problem 해결 결과를 묶어 전체 문제의 최종 솔루션을 도출!
🍻 큰 problem을 여러 개의 sub-problem으로 나누는 과정에서 recursion 재귀가 사용된다. 분할을 재귀로 구현하면서 나누고 더 이상 나눌 수 없는 sub-problem 각각 conquer(정복)한 다음 각 sub-problem별 conquer된 결과를 combine(결합)해 최종 결과를 도출하면 된다.
🍻 상황에 따라 combine 과정 없이 일부만 분할하고 일부만 정복한 뒤 바로 완료하는 유형도 존재(combine 결합이 반드시 포함되지는 x)
* example
Q. Finding the maximum
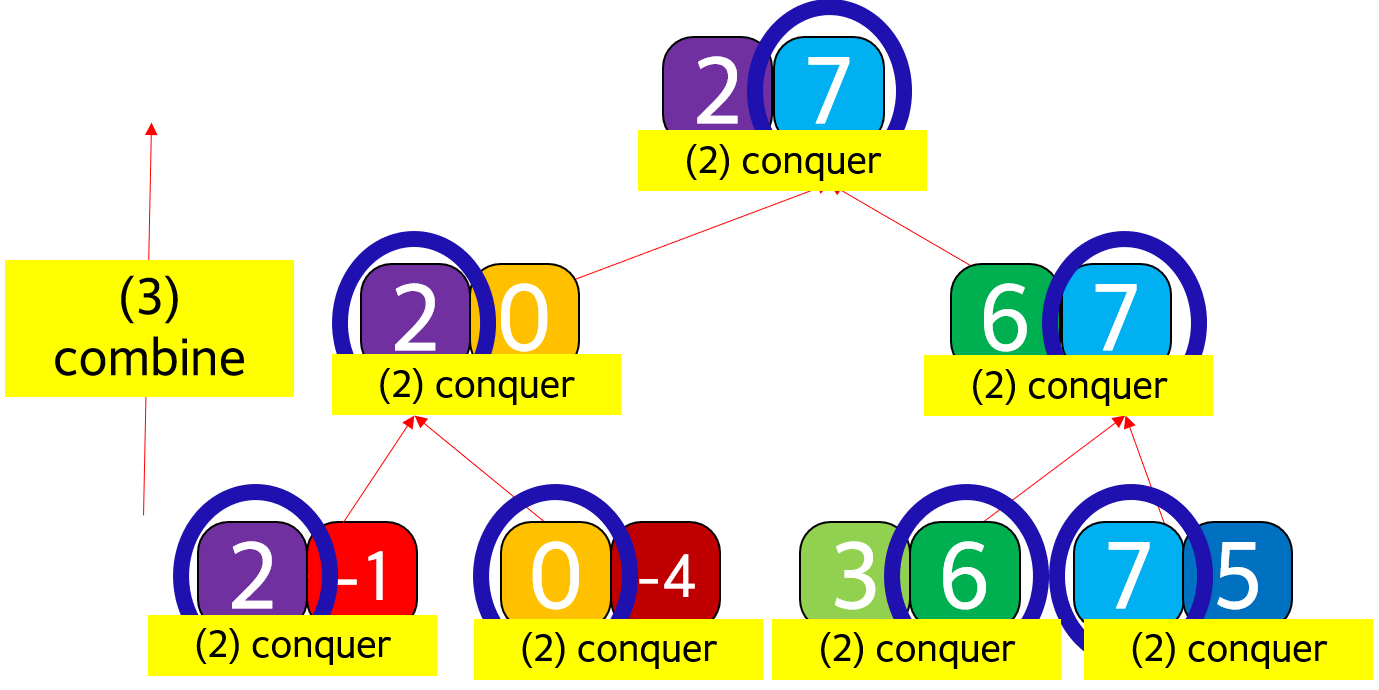
🍻 제일 간단한, 주어진 배열에서 최댓값을 찾는 과정을 생각해보자. 일단 Divide & Conquer 단계에 맞게 ① 먼저 맨 위의 긴 Array에서 절반으로 나누어나가는 과정 Divide를 아래와 같이 진행한다. 그 다음 ② 더 이상 나눌 수 없을 때 부터 Conquer를 시작해서 ③ 위로 올라가며 Combine을 해 나간다.
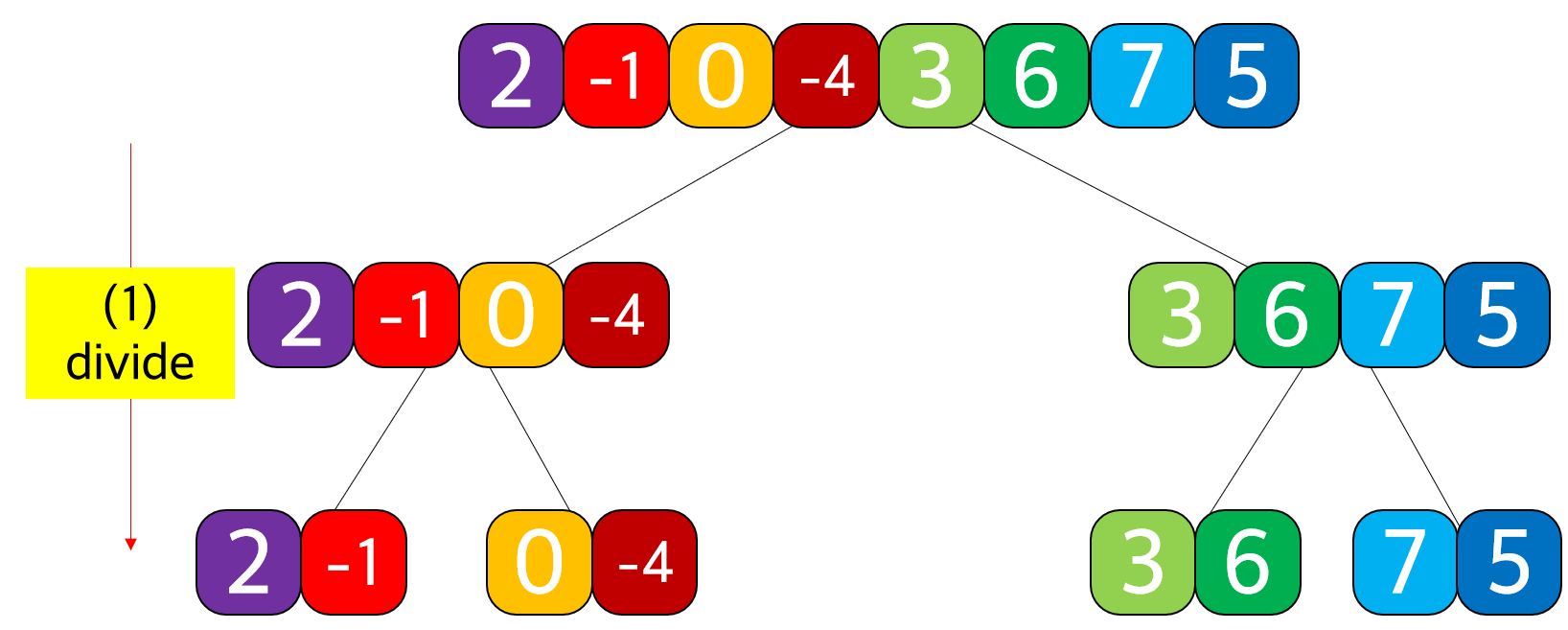
(1) divide: 일단 전체 list를 길이가 2 또는 1이 될 때까지 절반으로 sub-problem으로 나누어 나간다
(2) conquer: 최종적으로 나누어진 sub-problem의 각 list의 최댓값을 구한다. 최댓값을 구하는 건 max() 사용 없이 부등식으로 진행
(3) combine: 상황에 따라 분할정복 문제에서 divide&conquer만 진행할 수 있다. 해당 문제는 각각 conquer된 결과를 combine해 다시 위로 올라가며 또 conquer하고 combine하는 방식 계속 진행
def find_maximum(i,length):
if length <= 2:
if length == 1:
return l[i]
else:
if l[i] >= l[i+1]:
return l[i]
else:
return l[i+1]
if length%2 == 0:
left, right = find_maximum(i,length//2), find_maximum(i+length//2,length//2)
if left >= right:
return left
else:
return right
else:
left, right = find_maximum(i,length//2), find_maximum(i+length//2,length//2+1)
if left >= right:
return left
else:
return right
l = list(map(int,input('input your integers: ').split()))
print(find_maximum(0,len(l)))* properties
① 즉, DP는 여러 sub-problem이 서로 영향을 미치지만(subproblems are evaluated many times), DAC는 여러 sub-problem이 서로 영향을 주지 않는다(evaluated only once)
② 큰 공간 없이 cache memory 효율적인 사용
③ Quick Sort와 Merge Sort에 사용되는 분할-정복
④ 큰 problem을 여러 개의 sub-problems로 나눌 때 구현이 어려운 경우가 많다.
★ 분할정복으로 sub-problem으로 여러 번 나눌 때 재귀함수 내의 인자를 어떻게 설정할 지 고민하고, 재귀적으로 반복되는 부분을 찾아내자
* exercises
★ <BOJ S2 2630 색종이 만들기> ★
: 정사각형을 나누어서 하얀 영역, 파란 영역 색종이의 개수 구하면 된다.
★ <BOJ S2 1780 종이의 개수> ★
: 4등분이 아닌 9등분으로 divide
★ <BOJ S1 1074 Z> ★
: 4등분해서 찾고자 하는 곳만 depth 계속 divide하고 conquer한 뒤 바로 출력하고 종료
'Computer Science > Algorithms' 카테고리의 다른 글
| 🫂 Prefix Sum (1) | 2024.09.06 |
|---|---|
| 🍣 Fibonacci Sequence (0) | 2024.06.26 |
| 🚀 Power by Divide and Conquer (1) | 2024.06.06 |
| 🛣️ Shortest Path in an Unweighted Graph (1) | 2024.05.23 |
| ⛆ Flood Fill (0) | 2024.05.19 |


댓글