LIS(O(n^2))
「1」 LIS의 길이만 구할 경우
🍝 주어진 수열에서 가장 긴 증가하는 부분 수열을 구하는 문제. 이 때 부분 수열은 연속적일 필요 없고 unique할 필요도 없다. 띄엄띄엄 떨어진 원소 모음의 subsequence가 increasing하기만 하면 되며, increasing subsequence 중 최대 길이를 찾으면 된다. 예를 들어 [3, 10, 2, 1, 20]이 있다면 longest increasing subsequence는 [3, 10, 20] / [3,2]에서는 [3]과 [2] / [50, 3, 10, 7, 40, 80]에서는 [3, 7, 40, 80]이 있다. 이는 dp를 이용해서 쉽게 구할 수 있다. D[i]를 i번째 index에서 끝나는 LIS 길이라고 정의. 그러면 점화식은 아래와 같이 정의할 수 있다.
모든 0 ≤ j < i에 대하여, D[i] = max(D[i], D[j]+1) (if array[j] < array[i])
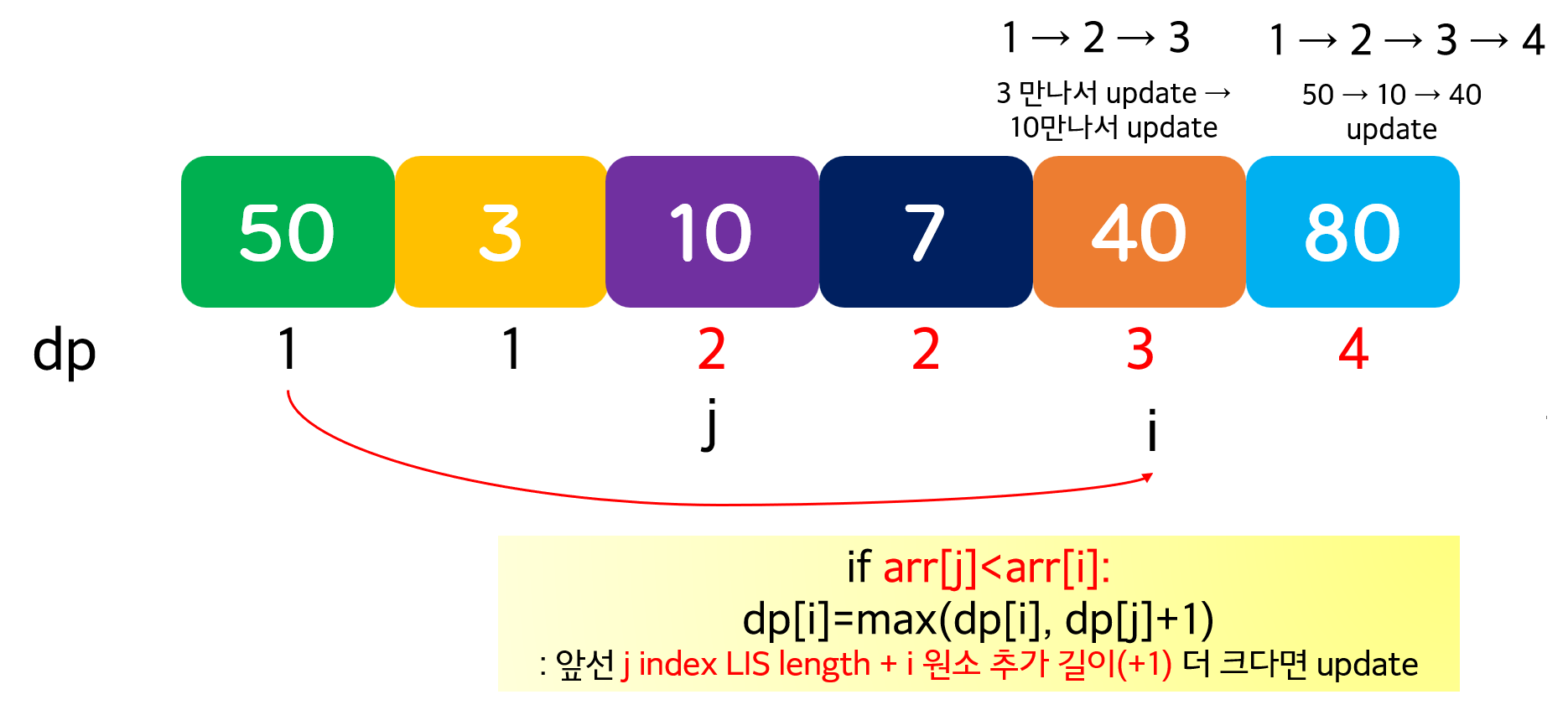
🍝 python code
: 원소 자체 1개 최소 LIS 길이 이므로 먼저 모든 원소 1로 초기화. 두 번 for문을 돌기 때문에 O(n^2)
#array length: N
#array name: A
dp=[1]*N
for x in range(1,N):
for y in range(x):
if A[y]<A[x]:
dp[x] = max(dp[x],dp[y]+1)
print(max(dp))
🍝 관련 문제
★ 교과서 문제) BOJ S2 11053 <가장 긴 증가하는 부분 수열> / BOJ S2 11722 <가장 긴 감소하는 부분 수열>
★ 응용 문제) BOJ S2 18353 <병사 배치하기> / BOJ G5 2565 <전깃줄>
★ LIS 응용 [Maximum Sum Increasing Subsequence(가장 큰 증가하는부분 수열)]) BOJ S2 11055 <가장 큰 증가하는 부분 수열>
「2」 LIS의 길이+내용 모두 구할 경우
🍝 위 dp에 길이 정보 + path 정보까지 같이 update 해나가면 된다. 다만 array[j] < array[i] 조건과(LIS 조건), dp[j][0] + 1 < dp[i][0](앞선 LIS 길이보다 더 큰 sequence 등장) 두 가지 조건만 만족하면 된다. path update는 현재 원소 array[i]를 해당 array D[j][1]에 붙여주면 된다.
모든 0 ≤ j < i에 대하여, D[i][0] = D[j][0] + 1, D[i][1] = D[j][1] + [array[i]] (if array[j] < array[i] and if dp[j][0] + 1 < dp[i][0])
🍝 관련 문제
★ 교과서 문제) BOJ G4 14002 <가장 긴 증가하는 부분 수열 4>

🍝 python code
: dp table의 원소는 [] list로 list의 첫번째 원소는 lis 길이 정보, 두번째 원소는 list 내용 정보로 모두 [1, A[i]]로 초기화
#array length: N
#array name: A
dp=[[1,[A[i]]] for i in range(N)]
for x in range(1,N):
for y in range(x):
if A[y]<A[x]:
if (dp[y][0] + 1) > dp[x][0]:
dp[x][0] = dp[y][0]+1
dp[x][1] = dp[y][1] + [A[x]]
print(max(dp)[0])
print(*max(dp)[1])LIS(O(nlogn))
🍝 O(n^2) 시간 복잡도가 아닌, 이분탐색을 활용해 O(nlogn))으로 풀 수 있다.
「1」 LIS의 길이만 구할 경우
: LIS에 들어가는 내용 상관 없이(이게 핵심) LIS의 길이 자체만 구할 수 있다.
① ans list 준비 (ans = [arr[0]]) → arr 첫 번째 원소 먼저 넣기
② arr의 두 번째 원소부터 for문 돌리기 (원소 x 가정)
③ 2가지 case로 나뉨
(1) ans list의 마지막 원소보다 크다 → ans 끝에 x 삽입
ex) ans가 [10, 30, 50] & x가 60이라 가정. 바로 붙임. 개수가 최대한 늘어나게 하는데만 관심 있으므로 추가할 수 있다면 바로 x 추가(ans 자체의 내용에는 관심 없다) → ans: [10, 30, 50, 60]
(2) ans list의 마지막 원소보다 작거나 같다 → x를 ans의 어떤 원소와 바꿀지 이분탐색 결정
ex) ans가 [10, 30, 50] & x가 50이라 가정. 세 번째 원소 50과 바꿈 → ans [10, 30, 50]
ex2) ans가 [10, 30, 50] & x가 40이라 가정. 세 번째 원소 50과 바꿈 → ans [10, 30, 40]
ex3) ans가 [10, 30, 50] & x가 5라 가정. 첫 번째 원소 10과 바꿈 → ans [5, 30, 50]
: 핵심은 ans의 마지막 원소 값을 최대한 줄여 ans의 길이를 최대한 늘리기. 길이만 관심 있으므로 ans 내의 내용이 어떤 값으로 바뀌는 지는 중요하지 않음.
★ 즉 x를 ans 내에 이분탐색으로 돌려 upper bound쪽(x<=l[mid])일 때 l[mid] 자리에 x로 update)에 대체
(최대한 list 맨 오른쪽의 원소가 작아야 이후 더 많은 원소를 넣을 수 있으므로! 다시 말하지만 원소의 값 자체는 중요치 않다)

④ 위 (2) 이분탐색(원소를 넣기 위한 적절한 위치를 탐색) 과정
: x의 upper-bound쪽의 원소 자리에 들어가야 하므로
(1) x<= l[mid]일 때 ans update하고 end = mid -1(ans update하는 쪽은 x<=l[mid]일 때)
(2) l[mid]<x일 때 start = mid + 1
∴ 따라서, 각 원소마다 최악으로 이분탐색한다고 가정할 때 시간 복잡도 O(nlogn)
🍝 python code
# array length: N
# array: A
# ans list update
#binary search
def binary_search(l, x):
start,end=0,len(l)-1
while start<=end:
mid=(start+end)//2
if x <= l[mid]:
end=mid-1
ans=mid
else:
start=mid+1
l[ans]=x
return l
#LIS
ans=[A[0]]
for x in range(1,N):
if ans[-1] < A[x]: #just add
ans.append(A[x])
else: #searching the spot
ans=binary_search(ans, A[x])
🍝 관련 문제
★ 교과서 문제) BOJ G2 12015 <가장 긴 증가하는 부분 수열 2> / BOJ G2 12738 <가장 긴 증가하는 부분 수열 3>
★ 응용 문제) BOJ G2 1365 <꼬인 전깃줄> / G2 2352 <반도체 설계>
「2」 LIS의 길이 + 내용까지 구할 경우
: 앞선 이분탐색 LIS(O(nlogn)) 알고리즘은 증가하는 가장 긴 부분 수열의 '길이'만 구할 수 있는 알고리즘이다. 최우선적으로 길이만 고려했어서 해당 수열 내에 어떤 내용이 들어가는 지는 중요치 않다. 이 때, 증가하는 가장 긴 부분 수열을 O(nlogn) 시간 복잡도 이내로 길이와 함께 구할 수 있다. index 저장 테크닉(index 저장용 리스트 1개 추가)만 있으면 충분히 구현 가능하다.
① 위 LIS(O(nlogn)) 이분탐색 알고리즘 그대로 구현
② 추가로 index 저장용 list ans_i 준비([1]부터 시작)
③ 모든 원소 for문 돌릴 때 두 가지 case에 따라 ans_i에 update
(1) ans list의 마지막 원소보다 크다 → cur_ans_l 변수 1씩 증가하면서(1 초기화) update되는 cur_ans_l을 ans_i에 삽입. 또는 update된 ans_num의 길이를 ans_i에 삽입해도 무방하다.
(2) ans list의 마지막 원소보다 작거나 같다 → binary_search 돌 때 최종적으로 구한 ans index + 1을 ans_i에 삽입. index가 1부터 시작하게 하였으므로 1 더해서 삽입
④ 완성된 ans_i는 아래 그림과 같이 당시 ans_num list에 들어간 위치(맨 왼쪽 1부터 시작) 번호를 뜻한다. 거꾸로 가장 큰 최댓값부터 왼쪽으로 향하면서 자신보다 1 낮은 숫자를 먼저 만나는 숫자가 실제 답 array에 들어간다. 아래의 경우 [3, 10, 40, 80]. 역으로 index를 추적해서 해당 조건에 맞는 숫자만 차례대로 출력하면 LIS의 내용까지 출력 가능

🍝 python code
#array A
#array length N
#binary search
def binary_search(l, i, x):
start,end=0,len(l)-1
while start<=end:
mid=(start+end)//2
if x <= l[mid]:
end=mid-1
ans=mid
else:
start=mid+1
l[ans]=x
i.append(ans+1)
return l, i
#LIS
ans_i=[1]
ans_num=[A[0]]
cur_ans_l=1
LIS=[]
for x in range(1,N):
if ans_num[-1] < A[x]: #just add
cur_ans_l+=1
ans_i.append(cur_ans_l)
ans_num.append(A[x])
else: #searching the spot
ans_num,ans_i=binary_search(ans_num, ans_i, A[x])
LIS_length = len(ans_num)
print(LIS_length)
for i in range(len(ans_i)-1,-1,-1):
if LIS_length == 0:
break
if ans_i[i] == LIS_length:
LIS.append(A[i])
LIS_length-=1
print(*reversed(LIS))
🍝 관련 문제
★ 교과서 문제) BOJ P5 14003<가장 긴 증가하는 부분 수열 5>
'Computer Science > Algorithms' 카테고리의 다른 글
| 🙃 Backtracking (0) | 2024.01.18 |
|---|---|
| 🧿 Dijkstra's (Shortest Path) Algorithm (1) | 2024.01.14 |
| 📡Kadane's Algorithm (0) | 2024.01.03 |
| 🔬 Parametric Search (1) | 2023.12.31 |
| 2️⃣Bipartite Graph (2) | 2023.12.21 |


댓글