intro
⛆ 플러드 필(Flood Fill) 알고리즘 이란, 주어진 2차원 그래프에서 연결영역의 개수 및, 각 연결영역의 연결 노드 개수를 구하는 알고리즘이다. 즉, 플러드 필은 DFS / BFS 그래프 순회 알고리즘을 응용한 알고리즘으로, 주어진 2차원 배열에서 연결 영역 관련 문제를 풀 때 사용된다.
⛆ 대표적인 케이스로, 연결 영역 개수 구하기, 가장 큰 영역 면적 구하기, 각 연결 영역 내의 노드 개수 구하기 등등이 나온다.
⛆ 시간 복잡도는 traverse할 2차원 그래프의 행 개수가 N이고 열 개수가 M이라면 O(NM), 공간 복잡도는 O(NM)이다.
1. 연결 영역 개수 구하기
ex) BOJ 4963 S2 <섬의 개수>
Q. 1과 0으로만 이루어진 2d array에서 1로만 이루어진 연결 영역, 즉 섬의 개수 구하기
DFS approach
⛆ DFS 재귀 기법을 활용해 풀 수 있다.
① 2차원 그래프 / visited 배열 준비(메모리 초과를 방지하기 위해 방문 시 해당 그래프의 노드를 다른 숫자로 바꾸는 경우도 있다)
② 2차원 그래프 각각 for문 돌면서 1일 경우만 dfs 진행. dfs 진행하면 재귀적으로 모든 연결된 1을 찾아 다른 숫자로 바꾸므로 첫 dfs를 진행할 때 섬의 수 count up
#graph
graph=[]
for _ in range(h):
graph.append(list(map(int,input().split())))
n=0
for i in range(h):
for j in range(w):
if graph[i][j] == 1:
dfs(graph,i,j)
n+=1
print(n)
③ dfs 함수에서 방문 처리를 다른 숫자 0으로 바꾸고(아니면 visited 배열 True로 바꾸거나 다른 값으로 바꾸기) 방향 벡터 dx, dy 선언 뒤 nx, ny 구해 nx, ny과 영역 내에 있고 연결된 1이라면 재귀적으로 dfs 다시 깊게 더 들어가기
def dfs(graph,x,y):
graph[x][y]=0
dx,dy=[-1,1,0,0,-1,-1,1,1],[0,0,-1,1,1,-1,1,-1,1]
for i in range(8):
nx,ny=x+dx[i],y+dy[i]
if 0<=nx<h and 0<=ny<w:
if graph[nx][ny] == 1:
dfs(graph,nx,ny)BFS approach
① 위 DFS와 동일
② 위 DFS와 동일. 각 node 2차원 그래프로 돌면서 1일 경우만 bfs 진행. dfs와 마찬가지로 bfs 돌면서 연결된 1을 모두 0으로 바꿈
#graph
graph=[]
for _ in range(h):
graph.append(list(map(int,input().split())))
n=0
for i in range(h):
for j in range(w):
if graph[i][j] == 1:
BFS(graph,(i,j))
n+=1
print(n)
③ bfs에서 먼저 시작 노드를 방문 처리로 숫자 0으로 바꾸고 queue에 넣기. while queue인 동안 왼쪽에서 빼서(appendleft()), 뺀 결과에서 방향 벡터 dx,dy 선언 뒤, 총 8 방향 각각 움직인 결과 범위 내에 있고 연결된 1이라면 queue 오른쪽에 append. 결과적으로 queue에 모든 노드가 없어질 때까지 찾을 수 있는 연결된 모든 곳 0 처리
def BFS(graph,start):
graph[start[0]][start[1]] = 0
queue=deque([start])
dx,dy=[-1,1,0,0,-1,-1,1,1],[0,0,-1,1,1,-1,1,-1,1]
while queue:
v = queue.popleft()
for i in range(8):
nx,ny=v[0]+dx[i],v[1]+dy[i]
if 0<=nx<len(graph) and 0<=ny<len(graph[0]):
if graph[nx][ny] == 1:
graph[nx][ny] = 0
queue.append((nx,ny))
★ 핵심은, 모든 노드를 for문으로 돌면서 연결 영역을 처음으로 구해야 할 경우 answer add up 하기 ★ (DFS/BFS 모두 적용)
examples
★ <BOJ S2 11724 연결 요소의 개수 / S2 1012 유기농 배추 / S2 4963 섬의 개수 / S2 5958 Space Exploration / S2 11123 양 한마리... 양 두마리...> ★
: 단순히 위 알고리즘 대로 구하기만 하면 된다
2. 각 영역 면적 구하기
앞에서는 연결 영역의 '개수'만 구했지만, 이제는 각 연결 영역 내의 노드 개수까지 구해보자. BFS의 경우 queue에 append할 때 n+=1 / DFS의 경우 DFS 함수를 재귀적으로 실행할 때 n+=1. DFS는 이 때 global n 전역 변수 설정
ex) BOJ 2667 S1 <단지번호 붙이기>
def dfs(graph,x,y):
global n
n+=1
graph[x][y]=0
dx,dy=[-1,1,0,0],[0,0,-1,1]
for i in range(4):
nx,ny=x+dx[i],y+dy[i]
if 0<=nx<N and 0<=ny<N:
if graph[nx][ny] == 1:
dfs(graph,nx,ny)
def bfs(graph,start_x,start_y,n,queue):
queue.append((start_x,start_y))
dx,dy=[-1,1,0,0],[0,0,-1,1]
while queue:
v = queue.popleft()
x,y=v[0],v[1]
for i in range(4):
nx,ny=x+dx[i],y+dy[i]
if 0<=nx<N and 0<=ny<N:
if graph[nx][ny] == 1:
graph[nx][ny]=0
n+=1
queue.append((nx,ny))
return n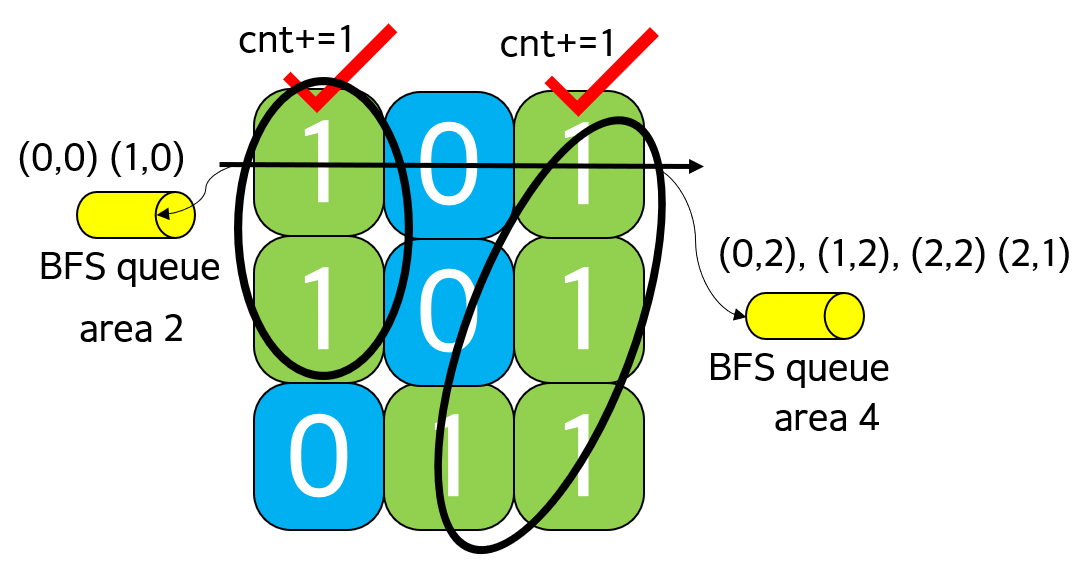
examples
① ★ BOJ S1 2667 단지번호붙이기 / S1 1926 그림 / S1 2468 안전 영역 / S1 1743 음식물 피하기 / S1 1303 전쟁 - 전투 / S1 3184 양 ★: 전형적인 연결영역 넓이와 개수 구하기 문제
② ★ BOJ S1 2583 영역 구하기 & S1 1325 효율적인 해킹: 해당 두 문제는 2차원 배열 만들 때만 주의 ★
③ ★ BOJ G4 14502 연구소 & G5 10026 적록색약: 연결영역을 찾기 위해 BFS를 여러 번 돌리기 ★
'Computer Science > Algorithms' 카테고리의 다른 글
| 🚀 Power by Divide and Conquer (1) | 2024.06.06 |
|---|---|
| 🛣️ Shortest Path in an Unweighted Graph (1) | 2024.05.23 |
| 🏘️Euler Sieve (1) | 2024.04.21 |
| 🥐Counting Sort (0) | 2024.04.17 |
| 🗼Tower of Hanoi (0) | 2024.04.09 |


댓글