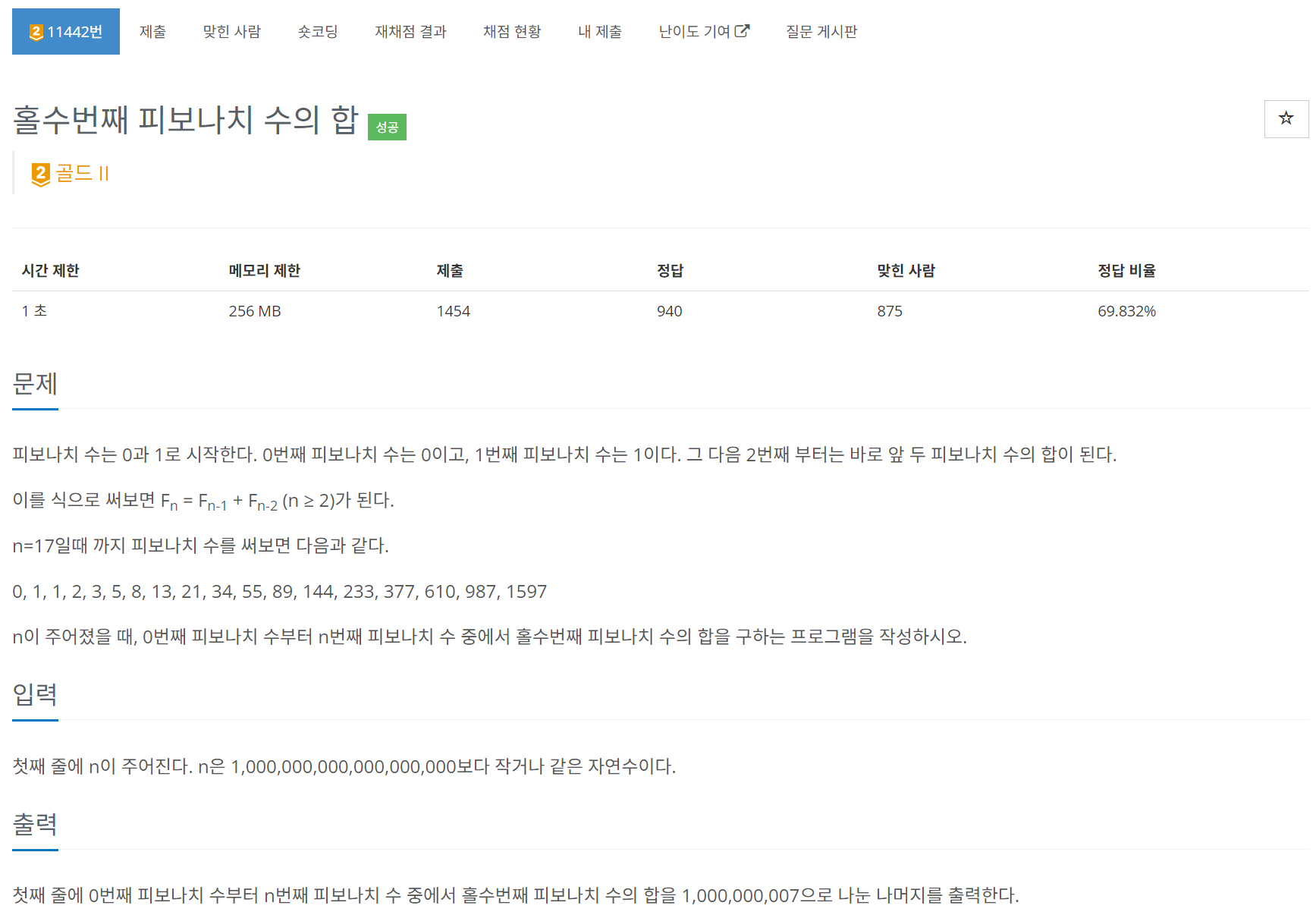
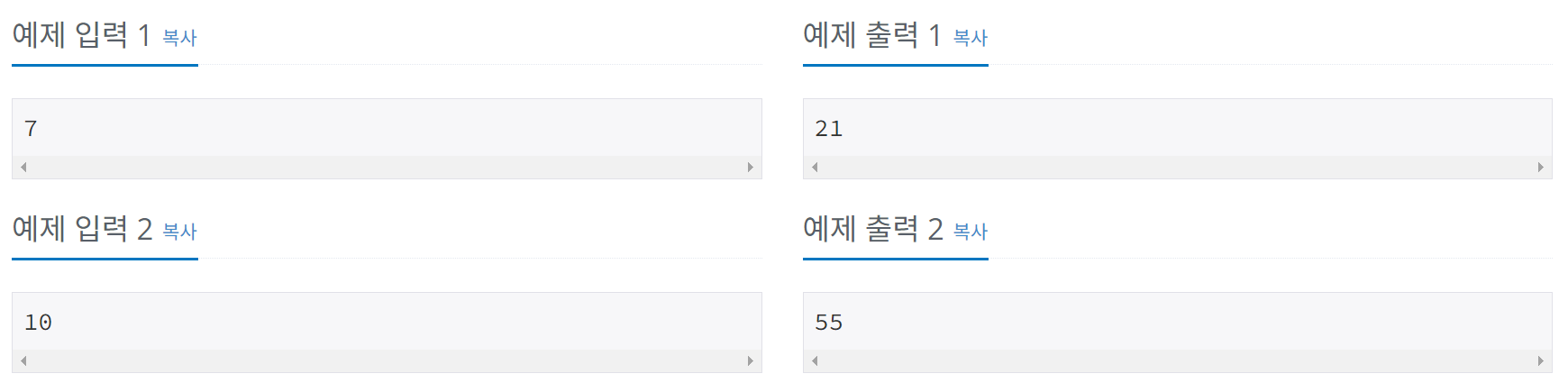
★ 11442 홀수번째 피보나치 수의 합 ★
n=int(input())
BIG=1_000_000_007
def get_power(a,b,c):
if b <= 1:
return [[a[0][0]%BIG,a[0][1]%BIG],[a[1][0]%BIG,a[1][1]%BIG]]
x = get_power(a,b//2,c)
if b % 2 == 0:
return prod(x,x)
else:
return prod(prod(x,x),a)
def prod(A,B):
a,b,c,d=A[0][0],A[0][1],A[1][0],A[1][1]
e,f,g,h=B[0][0],B[0][1],B[1][0],B[1][1]
return [[(a*e+b*g)%BIG,(a*f+b*h)%BIG],[(c*e+d*g)%BIG,(c*f+d*h)%BIG]]
core = [[1,1],[1,0]]
if n%2==1:
matrix = get_power(core,n,BIG)
print(matrix[0][0]%BIG)
else:
matrix = get_power(core,n-1,BIG)
print(matrix[0][0]%BIG)
🧚 F1부터 Fn까지의 홀수번째 피보나치 수의 합은 n이 홀수일 경우 F(n+1), n이 짝수일 경우 F(n)으로 구하면 된다. (피보나치 포스팅 증명 참조) 이 때 F 피보나치 값은 행렬의 분할정복 거듭제곱 알고리즘을 활용해 O(logn)만에 구하면 된다.
★ 11443 짝수번째 피보나치 수의 합 ★


n=int(input())
BIG=1_000_000_007
def get_power(a,b,c):
if b <= 1:
return [[a[0][0]%BIG,a[0][1]%BIG],[a[1][0]%BIG,a[1][1]%BIG]]
x = get_power(a,b//2,c)
if b % 2 == 0:
return prod(x,x)
else:
return prod(prod(x,x),a)
def prod(A,B):
a,b,c,d=A[0][0],A[0][1],A[1][0],A[1][1]
e,f,g,h=B[0][0],B[0][1],B[1][0],B[1][1]
return [[(a*e+b*g)%BIG,(a*f+b*h)%BIG],[(c*e+d*g)%BIG,(c*f+d*h)%BIG]]
core = [[1,1],[1,0]]
if n%2==0:
matrix = get_power(core,n,BIG)
else:
matrix = get_power(core,n-1,BIG)
ans=matrix[0][0]%BIG-1
print(ans if ans>=0 else ans+BIG)
🧚 n이 짝수일 경우 F1~Fn까지의 짝수번째 피보나치 수의 합은 F(n+1)-1, n이 홀수일 경우 짝수번째 피보나치 수의 합은 F(n)-1이다. 이 때 위 문제와 마찬가지로 F는 행렬의 분할정복을 이용한 거듭제곱으로 O(logn)만에 구하면 된다. 그리고 mod BIG 결과 -1이 나오면 BIG-1로 바꾸기
★ 7677 Fibonacci ★


BIG=10_000
def get_fibo_matrix(a,b,c,d,n):
if n == 1:
return [a%BIG,b%BIG,c%BIG,d%BIG]
else:
a1,b1,c1,d1=get_fibo_matrix(a%BIG,b%BIG,c%BIG,d%BIG,n//2)
a3 = ((a1%BIG)*(a1%BIG) + (b1%BIG)*(c1%BIG))%BIG
b3 = ((a1%BIG)*(b1%BIG) + (b1%BIG)*(d1%BIG))%BIG
c3 = ((c1%BIG)*(a1%BIG) + (d1%BIG)*(c1%BIG))%BIG
d3 = ((c1%BIG)*(b1%BIG) + (d1%BIG)*(d1%BIG))%BIG
if n%2==0:
return [a3,b3,c3,d3]
else:
a4 = ((a3%BIG)*(a%BIG) + (b3%BIG)*(c%BIG))%BIG
b4 = ((a3%BIG)*(b%BIG) + (b3%BIG)*(d%BIG))%BIG
c4 = ((c3%BIG)*(a%BIG) + (d3%BIG)*(c%BIG))%BIG
d4 = ((c3%BIG)*(b%BIG) + (d3%BIG)*(d%BIG))%BIG
return [a4,b4,c4,d4]
while 1:
n=int(input())
if n == 0:
print(0)
elif n == 1:
print(1)
elif n == -1:
break
else:
a,b,c,d=1,1,1,0
ans_list=get_fibo_matrix(a,b,c,d,n-1)
print(ans_list[0])
🧚 Fibonacci를 행렬을 이용한 분할정복 거듭제곱으로 O(nlogn)만에 구하면 된다.
★ 11444 피보나치 수 6 ★


n=int(input())
BIG = 1_000_000_007
def get_power(a,b,c):
if b <= 1:
return [[a[0][0]%BIG,a[0][1]%BIG],[a[1][0]%BIG,a[1][1]%BIG]]
x = get_power(a,b//2,c)
if b % 2 == 0:
return prod(x,x)
else:
return prod(prod(x,x),a)
def prod(A,B):
a,b,c,d=A[0][0],A[0][1],A[1][0],A[1][1]
e,f,g,h=B[0][0],B[0][1],B[1][0],B[1][1]
return [[(a*e+b*g)%BIG,(a*f+b*h)%BIG],[(c*e+d*g)%BIG,(c*f+d*h)%BIG]]
core = [[1,1],[1,0]]
matrix = get_power(core,n-1,BIG)
print(matrix[0][0]%BIG)
🧚마찬가지로 O(logn)만에 Fibonacci 수를 구하면 된다.
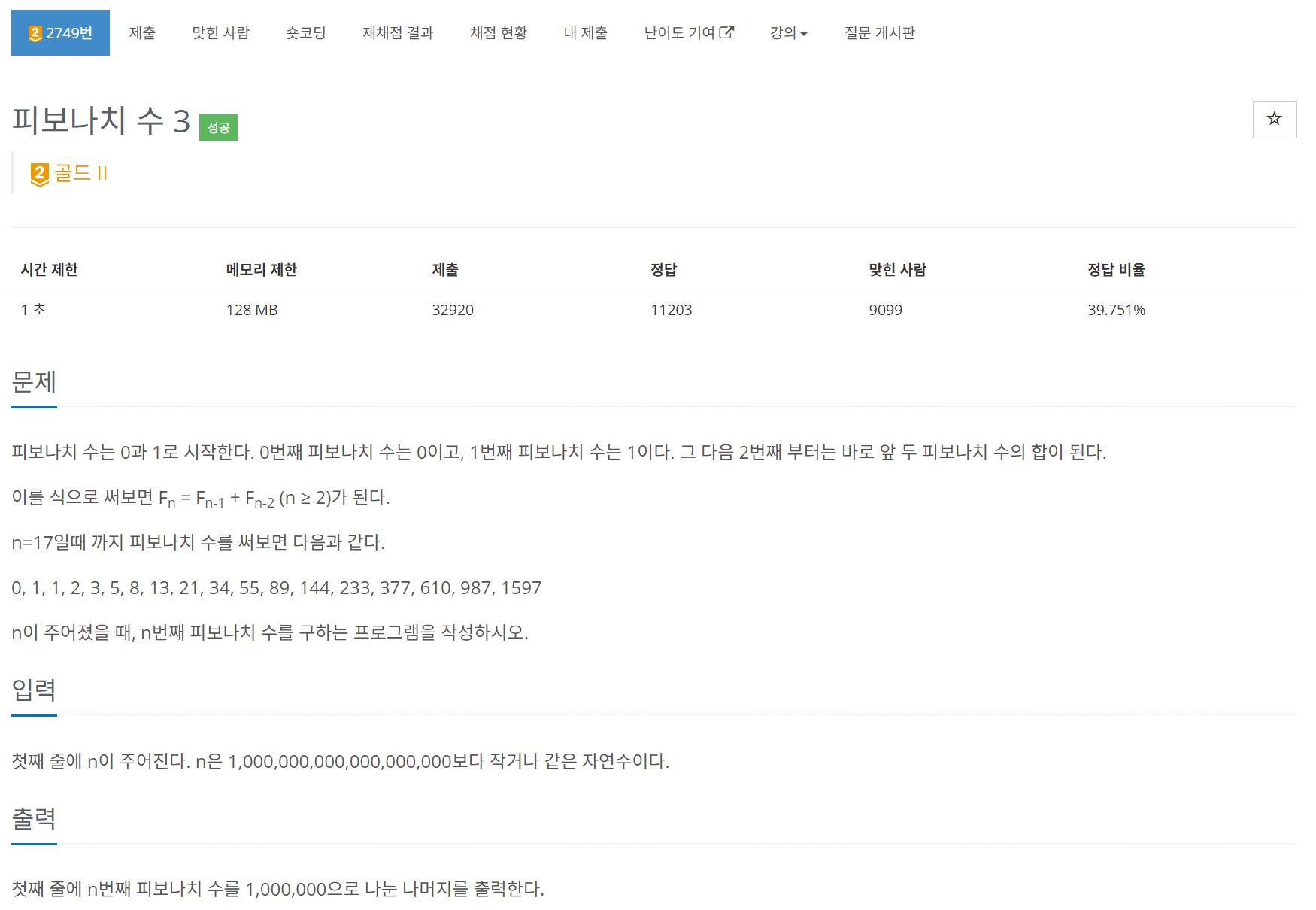
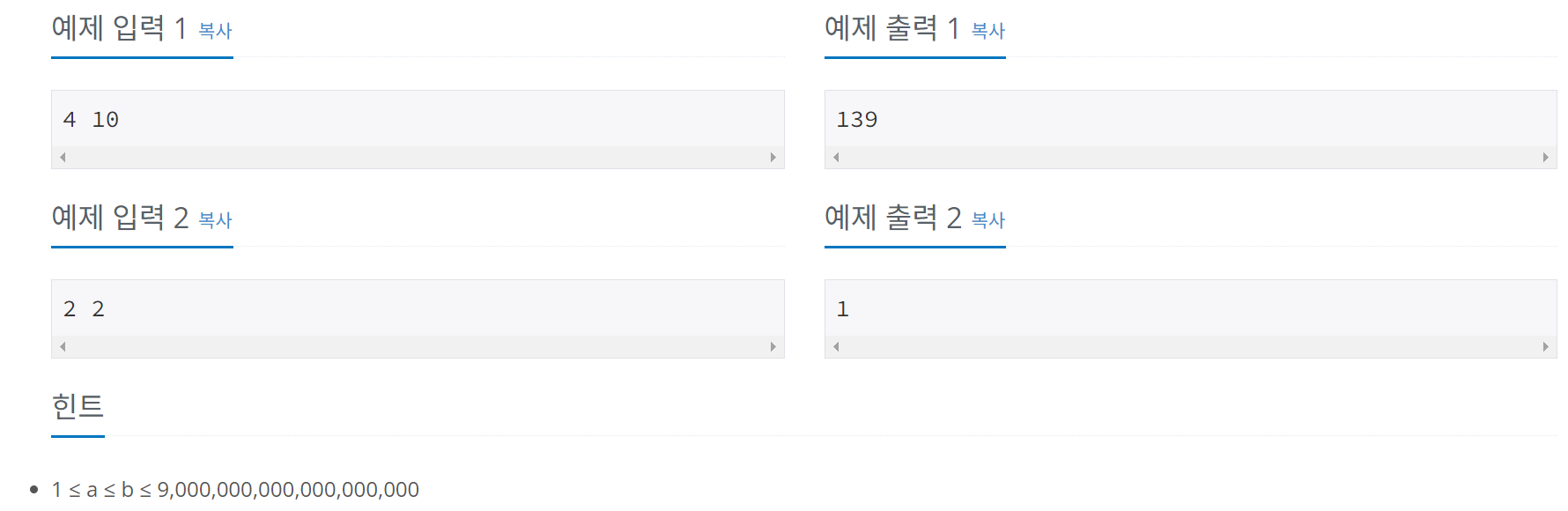
★ 2749 피보나치 수 3 ★

n = int(input())
M = 1_000_000 #M=10^k
k = 6
pi = 15 * (10**(k-1)) #pi(M) = 15*(10**(k-1))
if n == 1: print(1)
else:
fibo_arr=[0,1]
for x in range(2,n%pi+1):
fibo_arr.append((fibo_arr[-2]%M+fibo_arr[-1]%M)%M)
print(fibo_arr[-1])
🧚피사노 주기 성질에 의해 10^n으로 나눈 나머지는 15x(10^(n-1))임이 알려져 있다. 이를 활용해 피사노 주기 pi를 구하고 pi까지 돌려 fibonacci 수를 구할 수 있다. / 물론 O(logn) 전형적 행렬 활용한 분할정복 거듭제곱도 사용 가능
★ 2086 피보나치 수의 합 ★

a,b=map(int,input().split())
BIG = 1_000_000_000
def get_power(a,b,c):
if b <= 1:
return [[a[0][0]%BIG,a[0][1]%BIG],[a[1][0]%BIG,a[1][1]%BIG]]
x = get_power(a,b//2,c)
if b % 2 == 0:
return prod(x,x)
else:
return prod(prod(x,x),a)
def prod(A,B):
a,b,c,d=A[0][0],A[0][1],A[1][0],A[1][1]
e,f,g,h=B[0][0],B[0][1],B[1][0],B[1][1]
return [[(a*e+b*g)%BIG,(a*f+b*h)%BIG],[(c*e+d*g)%BIG,(c*f+d*h)%BIG]]
core = [[1,1],[1,0]]
if a == b:
matrix = get_power(core,a-1,BIG)
print(matrix[0][0]%BIG)
else: #sum(~b) - sum(~(a-1))
right_sum = (get_power(core,b+1,BIG)[0][0]-1)%BIG
left_sum = (get_power(core,a,BIG)[0][0]-1)%BIG
ans = right_sum - left_sum
print(ans%BIG if ans>=0 else (BIG+ans)%BIG)
🧚 a번째 항부터 b번째 항까지의 피보나치 수의 모든 합은 b번째 항까지의 피보나치 수의 합에서 (a-1)번째 항까지의 피보나치 수의 합을 빼면 된다. 뺀 결과가 0보다 작다면 ans에서 빼서 구하면 된다. 이 때 n번째 항까지의 피보나치 수의 합은 F(n+2)-1 사용
★ 13075 Fibonacci Sequence ★

import sys
input=sys.stdin.readline
BIG = 1_000_000_000
def get_power(a,b,c):
if b <= 1:
return [[a[0][0]%BIG,a[0][1]%BIG],[a[1][0]%BIG,a[1][1]%BIG]]
x = get_power(a,b//2,c)
if b % 2 == 0:
return prod(x,x)
else:
return prod(prod(x,x),a)
def prod(A,B):
a,b,c,d=A[0][0],A[0][1],A[1][0],A[1][1]
e,f,g,h=B[0][0],B[0][1],B[1][0],B[1][1]
return [[(a*e+b*g)%BIG,(a*f+b*h)%BIG],[(c*e+d*g)%BIG,(c*f+d*h)%BIG]]
core = [[1,1],[1,0]]
for _ in range(int(input())):
n=int(input())
matrix = get_power(core,n-1,BIG)
print(matrix[0][0]%BIG)
🧚 똑같이 10^9으로 나눈 Fibonacci 수 O(logn)만에 구하면 된다.
'PS - BOJ > 🥇' 카테고리의 다른 글
| ★Topology Sort Advanced - 2 Solved★ (0) | 2024.12.29 |
|---|---|
| ★Divide & Conquer Advanced I - 5 Solved★ (0) | 2024.06.15 |
| ★Math & Geometry Advanced I - 2 Solved★ (0) | 2024.04.27 |
| ★Implementation&Simluation Upper-Advanced I - 1 Solved★ (0) | 2024.03.03 |
| ★Stack & Queue & Deque Advanced I - 3 Solved★ (0) | 2024.02.24 |


댓글