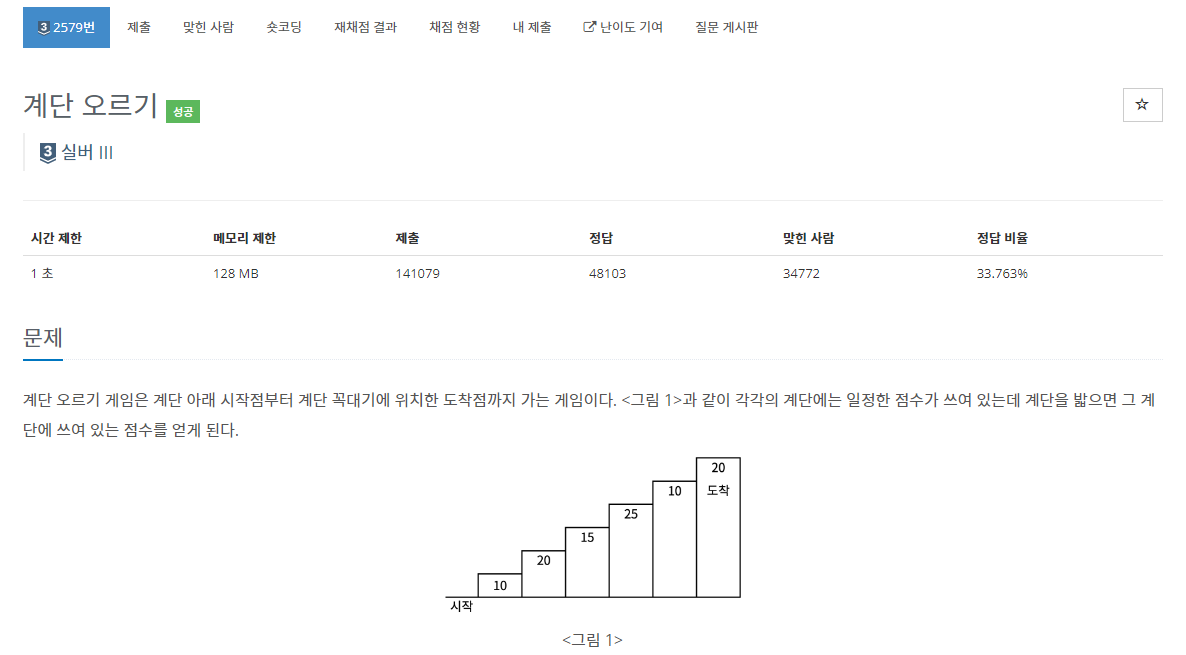
★ 2579 계단 오르기 ★

//2579
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <deque>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, stair,tmp;
cin >> N;
tmp = N;
vector<int> dp(N+1, 0);
vector<int> stairs = {0};
while(tmp--){
cin >> stair;
stairs.push_back(stair);
}
dp[1]=stairs[1];
dp[2]=stairs[1]+stairs[2];
dp[3]=stairs[3]+max(dp[1],stairs[2]);
for(int x = 4; x<N+1;x++){
dp[x] = stairs[x] + max(dp[x-2],dp[x-3]+stairs[x-1]);
}
cout << dp[N] << endl;
return 0;
}
🤡 점화식 a(n) = S(n) + max(a(n-2), a(n-3)+S(n-1))
🤡 vector로 1차원 배열 만들 때 크기와 초기화 코드 vector<int> dp(N+1, 0) 기억. 추가로 vector<int> stairs = {0}으로 미리 0 숫자 1개 집어넣고 push_back() 계속 진행 가능.
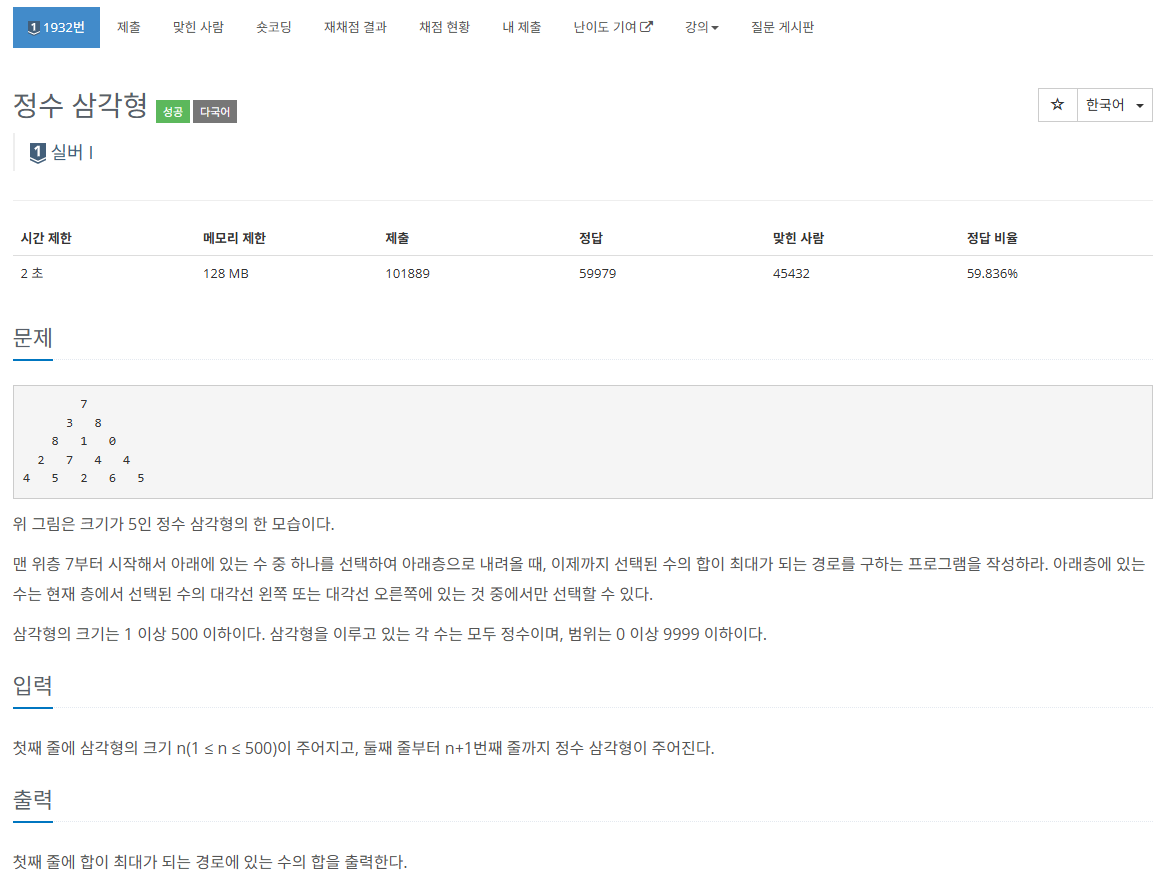
★ 1932 정수 삼각형 ★
//1932
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <deque>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, cnt = 1, num, cur_max = 0;
cin >> n;
vector<vector <int>> dp(n, vector<int>(n,0));
for(int j = 0; j < n; j++){
for(int i = 0; i < cnt; i++){
cin >> num;
if(i==0 || i == (cnt-1)){
if(j==0) dp[j][i] = num;
else{
if(i==0) dp[j][i] = num + dp[j-1][i];
else dp[j][i] = num + dp[j-1][i-1];
}
}
else{
dp[j][i] = num + max(dp[j-1][i],dp[j-1][i-1]);
}
}
cnt+=1;
}
for(int k: dp[n-1]){
cur_max = max(cur_max,k);
}
cout << cur_max << endl;
return 0;
}
🤡 2차원 dp는 vector<vector <int>> dp(n, vector<int>(n,0);으로 총 nxn vector 2d array 모두 0으로 초기화 진행할 수 있다.
🤡 그 다음은 문제의 점화식에 맞게 진행
'C, C++ Language > 🥈 BOJ' 카테고리의 다른 글
| (C++) ★Binary Search Intermediate I - 1 Solved★ (2) | 2024.11.15 |
|---|---|
| (C++) ★Backtracking Intermediate I - 3 Solved★ (2) | 2024.11.15 |
| (C++) ★Set/Map Upper-Intermediate I - 1 Solved★ (0) | 2024.11.15 |
| (C++) ★Stack & Queue & Deque Intermediate I - 4 Solved★ (0) | 2024.11.15 |
| (C++) ★Number Theory Intermediate I - 2 Solved★ (0) | 2024.11.15 |


댓글