1. Scalar
"단순히 변수로 저장되어 있는 숫자"
① vector 혹은 matrices에 곱해지는 경우 해당 값에 곱한 값으로 결정
② 단일숫자
③ 변수에 저장 시 소문자를 이용하여 표기
④ 실수 & 정수 모두 가능
⑤ 벡터의 크기를 맘대로 늘이는 걸 scaling한다고 해서 이 때 측정되는 크기를 scalar 라고 한다
2. Vector
intro
① 파이썬에서 주로 list로 사용된다. 숫자를 원소로 가지는 list 또는 array
② 아래 그림에서 벡터 x는 행벡터, xT는 열벡터

③ 파이썬에서는 코드로 아래와 같이 벡터를 표현할 수 있다. list 또는 np array로 여러 원소가 순서를 갖는 모음으로 표현 가능하다.
x = [1, 7, 2]
x = np.array([1, 7, 2])
④ 벡터에 있는 원소의 개수를 벡터의 차원이라 표현
⑤ 벡터는 공간에서 한 점으로 나타낸다. 1차원에서는 한 점, 2차원에서는 (x,y)로 한 점으로 표현. 3차원에서는 (x,y,z)로 표현. 실제 인공지능에서는 n차원 공간에서의 한 점으로 나타낸다. / 또한 벡터는 원점으로부터 상대적 위치를 표현한다고 할 수 있다.
⑥ 벡터에 숫자(스칼라)를 곱해주면 길이만 변한다. 이를 스칼라곱이라 부른다. 스칼라곱 결과 벡터의 각 원소가 곱한 결과로 나온다. 곱하는 스칼라가 1보다 크면 길이가 늘어나고, 1보다 작으면 길이가 줄어든다. 만약 0보다 작으면 벡터가 반대방향이 된다.
⑦ 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈 계산 가능. 또한 벡터끼리 같은 모양을 가지면 성분곱(Harmard product; element-wise product)을 계산할 수 있다. 아래 그림과 같이 표현 가능하다. 파이썬 코드에서는 np library에서 + - *로 편리하게 계산 가능


import numpy as np
x = np.array([1, 7, 2])
y = np.array([5, 2, 1])
print(x+y) #array([6, 9, 3])
print(x-y) #array([-4, 5, 1])
print(x*y) #array([5, 14, 2])
⑧ 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현. 예를 들어서 y벡터와 x벡터의 합은 y+x인 점으로 향하는 벡터라고 할 수 있다. 두 벡터의 뺄셈은 덧셈과 동일 의미. 예를 들어 y벡터 - x 벡터는 점 y에서 반대방향으로 x만큼 이동한 점을 향하는 벡터라고 할 수 있다. 아래 그림 참조

vector norm
① 벡터의 노름이란 원점에서부터의 거리를 뜻한다. L1 노름과 L2 노름으로 나눌 수 있으며 모두 n차원에서 성립. 원점으로부터의 거리는 벡터의 크기를 뜻하며 벡터 이름 앞 뒤에 ||기호를 붙인다.
② L1 노름은 각 성분의 변화량의 절댓값을 모두 더한다. 즉, 좌표계의 좌표평면에서 각 좌표축을 따라 움직이는 거리의 합. 예를 들어 (3,5) 벡터가 있다면 x축을 따라서 움직인 거리 3과 y축을 따라서 움직인 거리 5의 합인 8이 L1 norm이 된다.
③ L2 노름은 피타고라스 정리를 이용해 유클리드 거리를 계산한다. 즉, 원점에서 해당 벡터까지의 직선 거리를 뜻한다.

import numpy as np
def l1_norm(x):
return np.sum(np.abs(x))
def l2_norm(x):
return np.sqrt(np.sum(x*x)) # = np.linalg.norm
④ 노름의 종류에 따라 기하학적 성질이 달라진다.
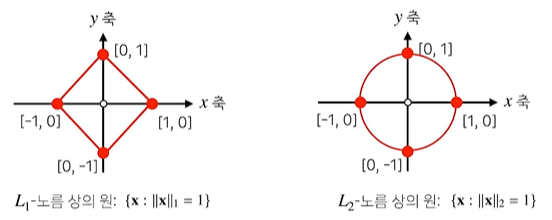
: 따라서 ML에선 각 성질들이 필요할 때가 각각 다르므로 둘 다 사용한다. 예를 들어서 L1-norm은 Robust 학습, Lasso 회귀에 사용되고, L2-norm은 Laplace 근사, Ridge 회귀에 사용된다. (자세한 건 추후 포스팅 참조)
⑤ 이 때 L1-norm과 L2-norm을 이용해 두 벡터 사이의 거리를 계산할 수 있다. 두 벡터 사이의 거리는 벡터의 뺄셈 사용.
⑥ 두 벡터 사이의 각도도 계산 가능하다. 제 2코사인 법칙에 의해 두 벡터 사이의 각도를 계산할수 있다.


: 두 벡터 사이의 거리는 x 벡터 또는 y 벡터를 평행이동해서 꼭짓점을 맞추어 덧셈 계산한, 즉 (x,y)의 L2 norm을 구하면 된다. 두 벡터 사이의 각도는 제2코사인법칙에 의해 L2 norm으로 위 공식대로 구하면 된다. L2 norm을 정의한 이유가 2차원이 아닌 일반적인 n차원에서도 구할 수 있게끔 만들어 놓은 식이라 생각하면 편하다.
아래 그림부터

→ 벡터의 element = 해당 vector의 고유한 특성
※ 벡터가 공간 상에서 갖는 위치는 해당 벡터의 고유한 특성 반영
→ 위치 정보를 이용해서 벡터 간의 유사도 계산 (위치가 비슷할수록 고유한 특성 유사 → 유사도가 크다)
→ 위치가 비슷한 정도: 거리로 계산

→ v1과 v2 서로 더 유사 (v1과 v3, 그리고 v2와 v3보다) (유사도 유클리디안 거리 L2 norm 계산 기준)
※ 벡터 간 유사도 별도 포스팅 참조! ※
※ L2 Norm을 이용해서는 두 vector 사이의 각도 계산 가능 (제2코사인법칙 활용)
※ np.linalg.norm() 사용 (코드 예시: 1개 종벡터의 L2 Norm)
2> 벡터의 내적
= "각 vector의 component를 곱한 뒤 합한 값" - 정사영(orthogonal projection)된 vector의 길이와 관련 있음
ex) v = [1,2,3,4] & x = [5,6,7,8]이라면 v⋅x = 1*5 + 2*6 + 3*7 + 4*8 = 70
→ 특징 1) 교환법칙이 적용됨 (a⋅b = b⋅a)
→ 특징 2) 분배법칙이 적용됨 (a⋅(b+c) = a⋅b+ a⋅c)
→ 특징 3) ** 벡터의 내적을 위해서는 두 벡터의 길이가 반드시 동일해야 함
※ 두 벡터의 덧셈은 다른 벡터로의 이동, 뺄셈은 반대 방향의 벡터를 더한 결과와 똑같음
※ x와 y의 내적이면 정사영된 벡터 x의 길이와 벡터 y의 길이와의 곱

※ 내적은 주로 두 벡터(데이터)의 유사도를 측정하는 데 보통 많이 사용함 ※
※ np.dot(a,b) 사용
a = np.array([1,2])
b = np.array([3,4])
print(np.dot(a,b)) #11
* 출처1) 대학원 사전교육
* 출처2) vector - https://www.youtube.com/watch?v=ArgTeYVuJUo
'Math & Linear Algebra > Concepts' 카테고리의 다른 글
| Probability fundamentals (0) | 2023.02.27 |
|---|---|
| SVD(Singular Value Decomposition) (0) | 2023.02.20 |
| eigendecomposition (0) | 2023.02.19 |
| vector similarity (0) | 2023.02.09 |
| Linear Equation & Linear System / Rank & det(A) (0) | 2023.02.01 |


댓글