4) Model Development
* A Model = a mathematical equation used to predict a value given one or more other values
- Relating one or more independent variables to dependant variables (ex) 'highway-mpg' -> model -> 'predicted price')
- the more relevant data have, the more accurate the model is
- more data is important
- different types of model) simple, multiple, and polynomial regression
(1) Simple & Multiple Linear Regression
* Linear Regression - refer to one independent variable to make a prediction
- the predictor(independent) variable x
- the target(dependent) variable y
- b0 - the intercept, b1 - the slope -

- fit -> predict
- hat on the y - denoting the model is an estimate -

- can use this model to predict values that haven't seen
- import linear_model from scikit-learn -
#fitting a Simple Linear Model
from sklearn.linear_model import LinearRegression
- create a Linear Regression Object using the constructor -
lm = LinearRegression()
- define the predictor variable & target variable -
X = df[['highway-mpg']]
Y = df['price']
- use lm.fit(X,Y) to fit the model, i.e find the parameters b0 and b1 -
lm.fit(X,Y)
- obtain a prediction -
Yhat = lm.predict(X) #the output is an array
- view the intercept & slope -
lm.intercept_
lm.coef_
(+참고)
Simple Linear Regression (concepts)
** 우리는 저번시간에 Supervised Learning - Regression - Linear Regression까지 concepts에 대해 배웠다 (↓↓↓↓↓↓ 하단 포스팅 참조 ↓↓↓↓↓↓) ML Supervised Learning → Regression → Linear Regr..
sh-avid-learner.tistory.com
* Multiple Regression - refer to multiple independent variables to make a prediction
- used to explain the relationship between: one continuous target(Y) variable & two or more predictor(X) variables
- b0 - the intercept, b1 - the coefficient or parameter of x1 and so on ... -

- extract the 4 predictor variables and store them in the variable Z -
Z = df[['horsepower', 'curb-weight', 'engine-size', 'highway-mpg']]
- train the model as before -
lm.fit(Z, df['price'])
- obatin a prediction -
Yhat = lm.predict(X)
- find the intercept & the coefficients -
lm.intercept_
lm.coef_ #the answer is given in array
(+참고)
Multiple Linear Regression Model (concepts+w/code)
✌️ 저번 시간에 feature가 1개인 단순선형회귀모델에 대해서 배웠다 ✌️ - 이론(개념) - Simple Linear Regression (concepts) ** 우리는 저번시간에 Supervised Learning - Regression - Linear Regression..
sh-avid-learner.tistory.com
(2) Model Evaluation using Visualization
* Regression Plot
= (a good estimate of) the relationship btw two variables
= (..) the strength of the correlation
= (..) the direction of the relationship (positive or negative)
- shows the combinaton of
≫ the scatterplot: each point represents a real different y + the fitted linear regression line ŷ
import seaborn as sns
sns.regplot(x="highway-mpg", y="price", data=df)
plt.ylim(0,)

* Residual Plot
= represents the error btw the actual value
- examine the difference between the actual value and predicted value
- obtain that value and plot on the vertical axis with the independent variable as the horizontal axis
- repeat the process
- expect to see the results to have zero mean
ex)

- (a) -

※ graph (a) analysis ↑>
→ distibuted evenly(randomly spread out) around the x-axis with similar variance
→ no curvature
→ suggests a linear model is appropriate
- (b) -

※ graph (b) analysis ↑>
→ there is a curvature
→ the values of the error change with x
→ not randomly spread out around the x-axis
→ suggests the linear assumption is incorrect (suggest a non-linear function)

※ graph (c) analysis ↑>
→ the variance of residuals increase with x (variance appears to change with x-axis)
→ not randomly spread out around the x-axis
→ suggests the linear assumption is incorrect (suggest a non-linear function)
import seaborn as sns
sns.residplot(df['highway-mpg'], df['price'])
→ first parameter = a series of dependent variable or feature
→ second parameter = a series of dependent variable or target
* Distribution Plot
= counts the predicted value verses the actual value
→ extremely useful for visualizing models with more than one independent variable or feature
→ the values of the targets & predicted values are continuous

- pandas convert them to a distribution (from histogram) -

- the actual values are in red; the fitted values that result from the model are in blue
- predicted values for prices ranging 40000 ~ 50000 are inaccurate / 10000 ~ 20000 are much closer to target value
- this suggests non-linear model may be suitable OR we need more data in the range
- after using multiple variables (features) -

- we can see predicted values are much closer to the actual values -
import seaborn as sns
ax1 = sns.distplot(df['price'], hist=False, color = "r", label = "Actual Value")
sns.distplot(Yhat, hist=False, color = "b", label = "Fitted Values", ax=ax1)(3) Polynomial Regression and Pipelines
Q) What do we do when our linear model is not the best fit for our data?
A) transform our data into a polynomial → then use linear regression to fit the parameter
* Polynomial Regression
= a special case of the general linear regression model
- useful for describing curvilinear relationships
(Curvilinear relationship = by squaring or setting higher-order terms of the predictor variables)

- quadratic (2nd order)
- cubic (3rd order)
- higher order
→ the degree of the regression makes a big difference and can result in a better fit if have the right value
→ the relationship btw the variable and the parameter is always linear
f = np.polyfit(x,y,3)
p = np.polyld(f)
print(p)

* Polynomial Regression with More than One Dimension
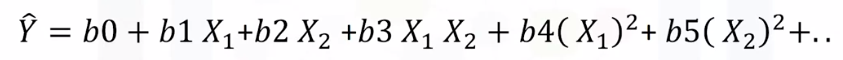
- Numpy's polyfit function cannot perform this type of regression
- we use the "preprocessing" library in scikit-learn
from sklearn.preprocessing import PolynomialFeatures
pr = PolynomialFeatures(degree=2, include_bias=False)
x_polly = pr.fit_transform(x[['horsepower','curb-weight']])
example) explained in the picture (for a easier understanding)

- as the data gets larger, we can normalize the data (standardscaler 관련 추후 포스팅)
- we can normalize each feature simultaneously
from sklearn.preprocessing import StandardScaler
SCALE = StandardScaler()
SCALE.fit(x_data[['horsepower','highway-mpg']])
x_scale = SCALE.transform(x_data[['horsepower','highway-mpg']])
(+) 참고
Polynomial Regression Model
* Linear Regression Model - 즉, y 종속변수와 x 독립변수(1개 또는 2개 이상)들 간의 관계가 선형인 경우를 뜻한다. 즉, x 독립변수의 증감 변화에 따라 y도 이에 상응하여 증감이 일정한 수치의 폭으로
sh-avid-learner.tistory.com
* Pipelines = a way to simplify code
- many steps to getting a prediction:
x → "Normalization" → "Polynomial transform" → "Linear Regression" → y hat

- simplify the process using a pipeline
- pipeline sequentially perform a series of transformations:
(1) transformations: normalization → polynomial transform
(2) prediction: linear regression
* through 'transformations' - normalize the data (X) and trasform into polynomial
(see 'polynomial regression with more then one dimension' above)
* through 'prediction' - based on the outcome of polynomial, we make the linear regression model
- import all the modules
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
- create a list of tuples
(the first element = the name of the estimator model / the second element = model constructor)
Input = [('scale',StandardScaler()), ('polynomial',PolynomialFeatures(degree=2), ... ('mode',LinearRegression())]
- input the list in the pipeline constructor
pipe=Pipeline(Input)
- train the pipeline by applying the train method to the pipeline object
- produce a prediction as well
Pipe.fit(df[['horsepower','curb-weight','engine-size','highway-mpg']],y)
yhat = Pipe.predict(X[['horsepower','curb-weight','engine-size','highway-mpg']])(4) R-squared and MSE for In-Sample Evaluation
→ In-Sample Evaluation = a way to numerically determine how good the model fits on dataset
* MSE (Mean Squared Error)
1) find the difference btw actual value Y and the predicted value Y hat, then square it
2) take all the squares and added it and divide them by the number of samples
from sklearn.metrics import mean_squared_error
mean_squared_error(df['price'],Y_predict_simple_fit)
Q) Does a lower MSE imply better fit?
A) Not neccesarily.
→ MSE for a Multiple Linear Regression Model will be smaller than the MSE for a Simple Linear Regression Model
(since the errors of the data will decrease when more variables are included in the model)
→ Polynomial regression will also have a smaller MSE than the linear regular regression
* R-squared (R^2)
= the Coefficient of Determination
- is a measure to determine how close the data is to the fitted regression line
- tells us what percent of the variability in the dependent variable is accounted for by the regression on the independent variable
(ex- R^2 = 1: dependent variables are completely explained by the movements in the independent variables)
ex)
- R^2 of 0.9986 -

→ more than 99 percent of the variability of the predicted variable is explained by the independent variables

- for the most part, it takes values btw 0 and 1
ex1)

→ the blue line = the regression line
→ the blue squares = the MSE of the regression line
→ the red line = the average of the data points
→ the red squares = the MSE of the red line
→ the area of the blue squares is much smaller than the area of the red squares

→ because the line is a good fit, the MSE is small (small numerator) in the regression line
→ taken to an extreme, this value tends to 0
→ for R^2, we get a value near 1 = the line is good fit for the data
ex2)

→ the area is almost identical
→ the ratio of the area is close to 1 (which means this line performs about the same as just using the average of the data points)
→ the R^2 is near 0 = this line did not perform well
X = df[['highway-mpg']]
Y = df['price']
lm.fit(X,Y)
lm.score(X,y)
# prints 0.496591188→ approximately 49.695% of the variation of price is explained by this simple linear model
※ if R^2 is negative, it is mainly due to overfitting
(+) 참고
All About Evaluation Metrics(1/2) → MSE, MAE, RMSE, R^2
** ML 모델의 성능을 최종적으로 평가할 때 다양한 evaluation metrics를 사용할 수 있다고 했음! ** (supervised learning - regression problem에서 많이 쓰이는 평가지표들) - 과정 (5) - 😙 그러면 차근차..
sh-avid-learner.tistory.com
(5) Prediction & Decision Making
Q) How can we determine if our model is correct?
- do the predicted values make sense
- visualization
- numerical measures for evaluation
A01) do the predicted values make sense?
lm.fit(df['highway-mpg'],df['prices'])
# train the model
lm.predict(np.array(30.0).reshape(-1,-1))
# predict the prica of a car with 30 highway-mpg
# Result $13771.30
→ the result is not negative, extremely high or low
→ can look at the coefficents using "lm.coef_"
import numpy as np
new_input = np.arange(1,101,1).reshape(-1,1)
yhat = lm.predict(new_input) #predict new values
# the output is a numpy array
A02) Numerical measures for evaluation
→ MSE
→ R^2
A03) Visualization (using graph)
5) Model Evaluation
= tells us how our model performs in the real world
(1) Model Evaluation & Refinement
- In-sample evaluation) tells us how well our model will fit the data used to train it
→ Problem) it does not tell us how well the trained model can be used to predict new data
→ Solution) split the data up: in-sample data or training data / out-of-sample evaluation or test set
(test set is used to approximate, how the model performs in the real world)
(+참고)
train vs. validation vs. test set
(! -- 매우 간단한 개념 짚고 넘어가는 목적 --!) * ML modelling할 때 주어진 train set로 모델을 구축하고 미리 주어진 data에서 일부 test set으로 뽑아 나중에 model에 집어넣어 예측값을 뽑거나 해당 모델
sh-avid-learner.tistory.com
* Spliting dataset
- the larger portion of data is used for training (usually)
- a smaller part is used for testing (usually)
- build & train the model with a training set
- use testing set to assess the performance of a predictive model
- when we have completed testing our model, we should use all the data to train the model to get the best performance
* train_test_split()
- x_data: features or independent variables
- y_data: dataset target
- test_size: a percentage of the data for the testing set
- random_state: number generator used for random sampling (a random seed for random data splitting)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.3, random_state = 0)
* Generalization Performance
→ Generalization error = a measure of how well our data does at predicting previously unseen data
Q. Lots of Training Data?
- Problem1) if we chose 90% of data as a training set, each of the results(randomly sampled in the dataset) are extremely different from one another (even if we get good approximation of the generalization error)
- Problem 2) if we use fewer data points to train the model & more to test the model, the accuracy of the generalization performance will be less, but the model will have great precision
A. Cross-Validation
(+참고)
Cross-Validation (concepts)
* 머신러닝을 위해서 무.조.건. 알아야 하는 CROSS-VALIDATION! 간단히 개념만 알아보ZA * - 2번 과정 - model selection에서 주로 많이 쓰이는 cross-validation 기법 - 🧐 PURPOSE? 'The purpose of cross..
sh-avid-learner.tistory.com
= most common out-of-sample evaluation metrics
- the dataset is split into K equal groups (each group is referred to as a fold)
- some folds can be used to train the model, and the other remaining folds can be used to test the model
- this is repeated until each partition is used for both training & testing

- we use the average result as the estimate of out-of-sample error
* cross_val_score()
= returns an array of scores (one for each partition the was chosen as the testing set)
- lr(first input parameter): the type of model we are using to do the cross-validation
- cv: the number of partitions
from sklearn.model_selection import cross_val_score
scores = cross_val_score(lr, x_data, y_data, cv=3)
np.mean(scores)
- can average the sample together(score is calculated using R-squared) using the mean function in numpy
+ we can use the negative squared error as a score by setting the parameter 'scoring' metric to 'neg_mean_squared_error'
-1 * cross_val_score(lre,x_data[['horsepower']], y_data,cv=4,scoring='neg_mean_squared_error')
- result) array([20254142.84026704, 43745493.26505169, 12539630.34014931, 17561927.72247591]) -
Q. We want to know the actual predicted values supplied by our model before the r-squared values are calculated?
A. cross_val_predict() function
* cross_val_predict()
= returns the prediction that was obtained for each element when it was in the test set
- a similar interface to cross_val_score()
from sklearn.model_selection import cross_val_predict
yhat = cross_val_predict(lr2e,x_data,y_data,cv=3)
- produces an array (9 y hats) -

(2) Overfitting, Underfitting, and Model Selection
Q) How can we pick the best polynomial order and problems that arise when selecting the wrong order polynomial?
* The goal of Model Selection
= to pick the polynomial to provide that the best estimate of the function y(x)
* Underfitting
→ the model is not complex enough to fit the data
→ there are so many errors

* Overfitting
→ the model does extremely well at tracking the training point
→ but performs poorly at estimating the function
- 16th polynomial regression -

- when there is little training data, the red box can be apparent
- estimated funcion oscillates, not tracking the function
- the model is too flexible & fits the noise rather than the function


- select the order that minimizes the test error
- on the left would be considered underfitting, on the right would be considered overfitting
- even if we select the best polynomial order, the error still occurs (a noise term)
→ a noise term) unpredictable, referred to as an irreducible error
Q) You have a linear model; the average R^2 value on your training data is 0.5, you perform a 100th order polynomial transform on your data then use these values to train another model. After this step, your average R^2 is 0.99. Which of the following is correct?
A) The results on your training data is not the best indicator of how your model performs; you should use your test data to get a better idea
(+참고)
Overfitting/Underfitting & Bias/Variance Tradeoff
1. 일반화(generalization) "In machine learning, generalization is a definition to demonstrate how well is a trained model to classify or forecast unseen data. Training a generalized machine learnin..
sh-avid-learner.tistory.com
(3) Ridge Regression
= a regression that is employed in a Multiple regression model when multicollinearity occurs
(Multicollinearity = when there is a strong relationship among the independent variables)
- very common with polynomial regression
- prevents overfitting
- controls the magnitude of the polynomial coefficients by introducing the parameter alpha
(+참고)
(L2 Regularization) → Ridge Regression (concepts)
** 우리는 저번 포스팅에서 Supervised Learning 중 Regression의 일종인 'linear regression'에 대해 학습했다. ☝️ 위 그림에서 보다시피 linear 선형 regression으로는 많은 종류의 model이 있음을 확인할..
sh-avid-learner.tistory.com
* Alpha
= a parameter we select before fitting / training the model

- as alpha increases, the parameters get smaller
→ alpha must be selected carefully
- if alpha is too large, the coefficients will approach zero & underfit the data
- if alpha is 0, overfitting is evident (alpha = 0.01 is most desirable in this case)
from sklearn.linear_model import Ridge
RidgeModel=Ridge(alpha=0.1)
RidgeModel.fit(X,y) #train the model
Yhat=RidgeModel.predict(X)
* Determining Alpha
- use some data for training -

- train) use some data for training
- predict) use validation data (used to select parameters like alpha)
- start with a small value of alpha -> calculate the r-squared and store the values
- repeat the value for a large value of alpha
- select the value of alpha that maximizes the R-squared
(we can use other metrics like mean-squared error)

- as the value of alpha increases, the value of R-squared (on the validation data) increases and converges at approximately 0.75 (validation data)
→ we select the maximum value of alpha (since higher values of alpha have little impact)
- conversely, as the value of alpha increases, the value of R-squared on the test data decreases
→ because the term alpha prevents overfitting
(4) Grid Search
- allows us to scan through multiple free parameters with few lines of code
- Scikit-learn) has a means of automatically iterating over the hyperparameters(term alpha in Ridge regression) using cross-validation (called Grid Search)

→ #1) takes the model or objects you would like to train and different values of hyperparameters
→ #2) calculate the mean squared error (or R-squared) for various hyperparameter values (let it choose the best values)
- select the hyperparameter that minimizes the error
* Three data sets
- split the data into training set, validation set, and test set
- training data) train the model for different hyperparameters
- validation data) we use to pick the best parameter
- test data) test the model performance using the test data
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
parameters1 = [{'alpha':[0.001,0.1,1,10,100,1000,10000,100000,1000000],'normalize':[True,False]}]
# structured in python dictionary
RR=Ridge() #create a ridge regression object
Grid1 = GridSearchCV(RR,parameters1,cv=4) #create a GridSearchCV object
# cv = 4 -> a number of folds
# use R-squared - default scoring method
Grid1.fit(x_data[['horsepower','curb-weight','engine-size','highway-mpg']],y_data)
# we fit the object
Grid1.best_estimator_
#fnd the best values for the free parameters (using the attribute 'best_estimator_')
scores=Grid1.cv_results_ #get the mean score of the validation data using the attribute 'cv_results_'
scores['mean_test_score']
BestRR=Grid1.best_estimator_
# can obtain the estimator with the best parameters and assign it toe the variable BestRR
# now test our model on the test data
BestRR.score(x_test[['horsepower', 'curb-weight', 'engine-size', 'highway-mpg']], y_test)
result) 0.8411649831036149
- the advantages of Grid Search) how quickly we can test multiple parameters -
for param,mean_val,mean_test inzip(score['params'],scores['mean_test_score'],scores['mean_train_score']):
print(param,"R^2 on test data:",mean_val,"R^2 on train data:",mean_test)
- printed as shown below -

* 전 내용 출처 <Data Analysis with Python (from Coursera)>
'Computer Science > Basics and Concepts' 카테고리의 다른 글
| Data Handling (0) | 2022.07.15 |
|---|---|
| feature scaling (0) | 2022.06.22 |
| Data Analysis with Python (1/2) (from Coursera) (0) | 2022.04.22 |
| in where? 🦸♀️ - AI examples (0) | 2022.04.17 |
| What is Data Science? (from Coursera) (0) | 2022.04.13 |


댓글