1. intro
★ 코딩의 대부분, 즉 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정
★ 어떤 알고리즘을 사용하더라도, 최종적으로는 구현을 해야 하기 때문에, 사실 모든 문제가 구현 유형이라고 할 수 있다.
★ 흔히 말하는 '구현' 문제는, 풀이를 떠올리는 건 쉽지만 직접 소스 코드로 옮기기 어려운 문제를 지칭
① 알고리즘은 간단하나, 코드가 지나칠 만큼 길어지는 문제
(프로그래밍 언어 종류에 따라 어려울 수도, 매우 쉬울 수도 있음)
② 실수 연산을 다루고, 특정 소수점 자리까지 출력해야 하는 문제
③ 문자열을 특정 기준에 따라서 끊어 처리해야 하는 문제
(python으로 매우 쉽게 풀 수 있는 경우 많고, 대표적으로 난이도 하의 1-2번 문제 위주)
④ 적절한 라이브러리를 찾아서 사용해야 하는 문제
(순열, 조합의 경우 python itertools library 사용 가능)
★ 무조건적으로 많은 문제를 푸는 것이 핵심!
★ 2차원 공간에서의 처리 많이 나옴 - 행렬 Matrix의 의미로 적용됨
→ 일반적으로 왼쪽 위 (0,0) 부터 시작함
→ 행은 x, 열은 y
→ 즉 아래로 내려갈수록 x값은 증가, 오른쪽으로 갈수록 y값이 증가(평상시 알고 있는 좌표 개념(유클리드 좌표)과 매우 다르니 주의!)

for i in range(5):
for j in range(5):
print('(', i, ',', j, ')', end=' ')
print()
★ 시뮬레이션이나 완전탐색 문제에서는 2차원 공간에서의 방향 vector가 자주 활용
(시뮬레이션, 완전탐색, 구현 서로 비슷한 개념이므로 한꺼번에 '구현(implementation)'이라 부르면 OK)
→ 특정 위치에서 동서남북 자유롭게 방향 이동
ex) 2차원 공간에서 현재 위치가 (2,2)에 있다고 했을 때

#East, North, West, South
dx = [0,-1, 0, 1]
dy = [1, 0, -1, 0]
x,y = 2,2
for i in range(4):
nx = x+dx[i]
ny = y+dy[i]
print(nx,ny)
#2 3
#1 2
#2 1
#3 2: dx와 dy 각각 x와 y축 별로 이동을 정의해 상하좌우로 움직이는 dx와 dy 방향벡터를 만들어 움직인 뒤의 좌표 결과들을 출력!
2. 대표유형
(1) simulation - 상하좌우
Q. 여행가 A는 N x N 크기의 정사각형 공간 위에 서 있다. 이 공간은 1 x 1 크기의 정사각형으로 나누어져 있다. 가장 왼쪽 위 좌표는 (1,1)이며, 가장 오른쪽 아래 좌표는 (N,N)에 해당한다. 여행가 A는 상,하,좌,우 방향으로 이동할 수 있으며, 시작 좌표는 항상 (1,1)이다. 우리 앞에는 여행가 A가 이동할 계획이 적힌 계획서가 놓여 있다.
→ 계획서에는 하나의 줄에 띄어쓰기를 기준으로 하여, L, R, U, D 중 하나의 문자가 반복적으로 적혀 있다. 각 문자의 의미는 다음과 같다
→ L: 왼쪽으로 한 칸 이동, R: 오른쪽으로 한 칸 이동, U:위로 한 칸 이동, D: 아래로 한 칸 이동
※ 이 때 여행가 A가 N x N 크기의 정사각형 공간을 벗어나는 움직임은 무시된다. 예를 들어 (1,1)의 위치에서 L 혹은 U를 만나면 무시된다.
(예를 들어 R - R - R - U - D - D에서 U일 때 공간 밖을 벗어나므로 무시. (1,1)에서 시작하므로 최종 도착점은 (3,4))

🏃♂️ 내 풀이>
N = int(input())
plans = [d for d in input().split()]
#L,R,U,D
dx = [0,0,-1,1]
dy = [-1,1,0,0]
#x,y
x,y = 1,1
for plan in plans:
if plan == 'L':
if (y + dy[0]) == 0:
continue
y = y + dy[0]
elif plan == 'R':
if (y + dy[1]) > N:
continue
y = y + dy[1]
elif plan == 'U':
if (x + dx[2]) == 0:
continue
x = x + dx[2]
else: #plan == 'D'
if (x + dx[3]) > N:
continue
x = x + dx[3]
print(x,y)
#time complexity O(len(plans))
🏃♂️ 이코테 풀이>
n = int(input())
x,y = 1,1
plans = input().split()
dx = [0,0,-1,1]
dy = [-1,1,0,0]
move_types = ['L', 'R', 'U', 'D']
for plan in plans:
for i in range(len(move_types)):
if plan == move_types[i]:
nx = x + dx[i]
ny = y + dy[i]
if nx < 1 or ny < 1 or nx > n or ny > n:
continue
x,y = nx, ny
print(x,y)
→ move_types의 length가 4로 고정되어 있어서 한 번 더 for문을 돌려도 time complexity의 차이가 없다.
→ 비교 시 여러 list에 넣고 for ~ range(len~)문을 이용해 쉽고 간단한 로직으로 풀리는 경우 많으니 위의 로직 기억하기!
(일일이 if문 조건분기보다 위와 같은 code로 좀 더 깔끔하게 짤 수 있다는 점)
(2) brute-force - 시각
Q. 정수 N이 입력되면 00시 00분 00초부터 N시 59분 59초까지의 모든 시각 중에서 3이 하나라도 포함되는 모든 경우의 수를 구하는 프로그램을 작성하세요. 예를 들어 1을 입력했을 때 다음은 3이 하나라도 포함되어 있으므로 세어야 하는 시각입니다.
- 00시 00분 03초
- 00시 13분 30초
반면에 다음은 3이 하나도 포함되어 있지 않으므로 세면 안되는 시각입니다.
- 00시 02분 55초
- 01시 27분 45초

🏃♂️ 내 풀이>
N = int(input())
without_three = 0
with_three = 60*60 #N == 3, 13, 23
start = 5959
while start >= 3:
stringed = str(start).zfill(4)
if stringed[-2:] == '99':
start -= 40
if '3' == stringed[0]:
without_three += 600
start -= 1000
elif '3' == stringed[1]:
without_three += 60
start -= 100
elif '3' == stringed[2]:
without_three += 10
start -= 10
elif '3' == stringed[3]:
without_three += 1
start -= 1
else:
start -= 1
if N<=2:
print(without_three*(N+1))
elif N<=12:
print(without_three*N + 3600)
elif N<=22:
print(without_three*(N-1) + 3600*2)
else:
print(without_three(N-2) + 3600*3)
🏃♂️ 이코테 풀이>
h = int(input())
count = 0
for i in range(h+1):
for j in range(60):
for k in range(60):
if '3' in str(i) + str(j) + str(k):
count += 1
print(count)
→ 전형적인 브루트-포스 알고리즘으로 가능한 모든 시각의 경우를 하나씩 모두 조건과 따져서 풀 수 있는 문제
→ 하루는 86400초이므로 모든 경우의 수는 86400가지 - 따라서 단순히 1씩 증가시키면서 3의 포함 여부 확인
※ python3의 경우 1초에 2천만번의 연산을 수행 가정으로 바람직함 (86400은 많은 경우의 수가 아님)
→ 위 for문을 세 번이나 중첩했지만 최대 범위는 23시의 경우 23*60*60 - time complexity로 따져도 큰 범위가 아니므로 충분히 완전탐색으로 풀어도 가능!
(3) 2차원 배열 - 왕실의 나이트
Q. 행복 왕국의 왕실 정원은 체스판과 같은 8x8 좌표 평면입니다. 왕실 정원의 특정한 한 칸에 나이트가 서 있습니다. 나이트는 매우 충성스러운 신하로서 매일 무술을 연마합니다. 나이트는 말을 타고 있기 때문에 이동을 할 때는 L자 형태로만 이동할 수 있으며 정원 밖으로는 나갈 수 없습니다. 나이트는 특정 위치에서 다음과 같은 2가지 경우로 이동할 수 있습니다.
- 수평으로 두 칸 이동한 뒤에 수직으로 한 칸 이동하기
- 수직으로 두 칸 이동한 뒤에 수평으로 한 칸 이동하기
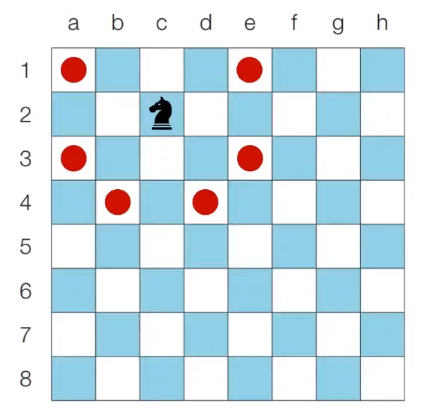
이처럼 8x8 좌표 평면 상에서 나이트의 위치가 주어졌을 때 나이트가 이동할 수 있는 경우의 수를 출력하는 프로그램을 작성하세요. 왕실의 정원에서 행 위치를 표현할 때는 1부터 8로 표현하며, 열 위치를 표현할 때는 a부터 h로 표현합니다.
- c2에 있을 때 이동할 수 있는 경우의 수는 6가지입니다. (아래 그림 참조)

🏃♂️ 내 풀이>
pos = input()
row = 'abcdefgh'
x,y = int(pos[1]),row.index(pos[0])+1
cnt = 0
#l,r,u,d
dx=[0,0,-1,1]
dy=[-1,1,0,0]
n_pos = []
n_pos.append((x + 2*dx[0] + dx[2], y + 2*dy[0] + dy[2])) #l*2 + u*1
n_pos.append((x + 2*dx[0] + dx[3], y + 2*dy[0] + dy[3])) #l*2 + d*1
n_pos.append((x + dx[0] + 2*dx[2], y + dy[0] + 2*dy[2])) #l*1 + u*2
n_pos.append((x + dx[0] + 2*dx[3], y + dy[0] + 2*dy[3])) #l*1 + d*2
n_pos.append((x + 2*dx[1] + dx[2], y + 2*dy[1] + dy[2])) #r*2 + u*1
n_pos.append((x + 2*dx[1] + dx[3], y + 2*dy[1] + dy[3])) #r*2 + d*1
n_pos.append((x + dx[1] + 2*dx[2], y + dy[1] + 2*dy[2])) #r*1 + u*2
n_pos.append((x + dx[1] + 2*dx[3], y + dy[1] + 2*dy[3])) #r*1 + d*2
for after_pos in n_pos:
if after_pos[0] < 1 or 8 < after_pos[0] or after_pos[1] < 1 or 8 < after_pos[1]:
continue
cnt += 1
print(cnt)
🏃♂️ 이코테 풀이>
→ 총 8가지 방향에 대한 방향 벡터를 정의
input_data = input()
row = int(input_data[1])
column = int(ord(input_data[0])) - int(ord('a')) + 1 #ascii
steps = [(-2,-1), (-1,-2), (1,-2), (2,-1), (2,1), (1,2), (-1,2), (-2,1)]
result = 0
for step in steps:
next_row = row + step[0]
next_column = column + step[1]
if next_row>=1 and next_row<=8 and next_column>=1 and next_column<=8:
result += 1
print(result)
→ 방향벡터 dx, dy와 다르게 이동하는 8가지의 방향을 () 형태로 각각 x,y 이동 양을 정해 list로 만든 뒤, 각각 이동했을 때 2차원 배열을 벗어나는 지 확인만 하면 끝!
→ ASCII 코드를 사용해 연속한 알파벳에 숫자를 부여하는 ord()도 기억
→ 전형적인 2차원 배열 구현 문제! 이것으로 2차원 배열에 처음으로 익숙해지기!
(4) 문자열 구현 - 문자열 재정렬
Q. 알파벳 대문자와 숫자(0~9)로만 구성된 문자열이 입력으로 주어집니다. 이 때 모든 알파벳을 오름차순으로 정렬하여 이어서 출력한 뒤에, 그 뒤에 모든 숫자를 더한 값을 이어서 출력합니다. 예를 들어 K1KA5CB7이라는 값이 들어오면 ABCKK13을 출력합니다.

🏃♂️ 내 풀이>
string = input()
alphas = []
numbers = []
for s in string:
if s.isdigit() == False:
alphas.append(s)
else:
numbers.append(int(s))
alphas.sort()
for alpha in alphas:
print(alpha, end='')
print(sum(numbers))
🏃♂️ 이코테 풀이>
data = input()
result = []
value = 0
for x in data:
if x.isalpha():
result.append(x)
else:
value += int(x)
result.sort()
if value != 0:
result.append(str(value))
print(''.join(result))
→ 실제 풀이와 거의 비슷. 다만 for문을 출력을 위해 돌리지 않고, 한 번에 join을 사용해 실행시간을 더 단축시켰음을 볼 수 있음
→ 문제 지시사항 그대로 푸는 전형적인 '구현 문제'
'Computer Science > Algorithms' 카테고리의 다른 글
| 👀 Binary Search 👀 (2) | 2022.12.06 |
|---|---|
| understanding pesudo-code of QuickSort (0) | 2022.12.05 |
| DFS / BFS (0) | 2022.10.14 |
| 🧭Recursion (0) | 2022.09.27 |
| Greedy (0) | 2022.09.12 |


댓글