① DFS(Depth-First Search)
⚡️ 먼저 DFS는 깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
⚡️ 스택 자료구조(또는 재귀함수)를 이용하며, 구체적인 동작 과정은 아래와 같다
① 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
② 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
③ 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
⚡️ 동작 예시
※ 먼저 방문노드 / 방문기준을 정하는 게 중요
→ 문제마다, 상황마다 방문노드 정하는 기준은 제각각이다
ex) 예시에서는 방문노드는 1, 방문기준은 번호가 낮은 인접노드부터 방문한다고 시작한다.
① [Step 0] 그래프를 준비한다
* 방문기준은 인접한 노드가 여러 개 일때 어떤 노드부터 방문할 지 그 방문기준을 세우는 것을 말한다.
* 간선은 방향이 없는 무방향 간선으로 간주
→ 시작 노드: 1
② [Step 1] 시작 노드인 '1'을 삽입하고 방문처리를 한다.
③ [Step 2] 스택의 최상단 노드인 '1'에 방문하지 않은 인접 노드 '2', '3', '8'이 있다.
→ 이 중에서 가장 작은 노드인 '2'를 스택에 넣고 방문처리 진행
④ [Step 3] 스택의 최상단 노드인 '2'에 방문하지 않은 인접 노드 '7'이 있다.
→ 따라서 7번 노드를 스택에 넣고 방문 처리 진행
⑤ [Step 4] 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '6', '8'이 존재
→ 이 중 가장 작은 노드인 '6'을 스택에 넣고 방문 처리 진행
→ 이렇게 DFS는 깊이 우선 탐색으로 진행하기에 그래프에서 가장 깊은 부분을 우선적으로 탐색하게 됨
⑥ [Step 5] 스택의 최상단 노드인 '6'에 방문하지 않은 인접노드가 없다.
→ 따라서 스택에서 '6'번 노드를 꺼낸다.
⑦ [Step 6] 스택의 최상단 노드인 '7'에 방문하지 않은 인접노드 '8'이 존재한다
→ 따라서 '8'번 노드를 스택에 넣고 방문 처리 진행





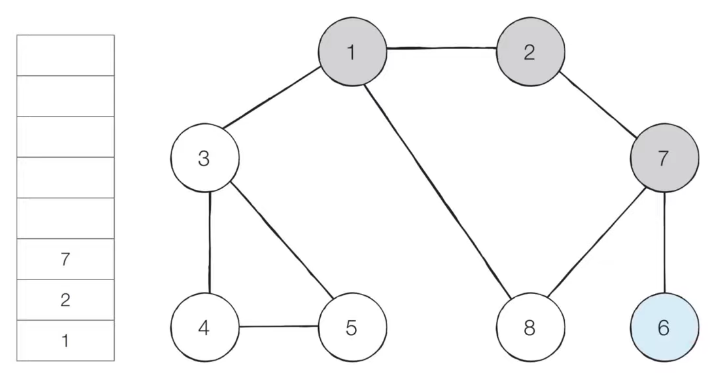


⑧ 이러한 과정을 반복하였을 때 전체 노드의 탐색 순서(스택에 들어간 순서)는 다음과 같다
≫ 탐색순서: 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5
※ 탐색 방향을 구체적으로 돌아보면
▶ 1 → 2 → 7 → 6으로 갔다가
▶ 6에서 방문하지 않은 노드가 없으므로 꺼냄
▶ 최상단 노드 7 에서 방문하지 않은 노드 8로 갔다가 (7 → 8)
▶ 8에서도 방문하지 않은 노드가 없으므로 꺼냄
▶ 최상단 노드 7에서도 없으므로 꺼냄
▶ 6에서도 없으므로 꺼냄
▶ 2에서도 없으므로 꺼냄
▶ 1 → 3 → 4 → 5로 갔다가
▶ 최상단 노드 5에서 방문하지 않은 노드가 없으므로 꺼냄 → 역으로 쭈욱
▶ 정리) 1 → 2 → 7 → 6 → 7 → 8 → 7 → 2 → 1 → 3 → 4 → 5 → 4 → 3 → 2 → 1
→ 이렇게 최대한 깊게 들어가는 방향으로 동작하기 때문에 스택 대신 재귀함수로도 코드로 구현이 가능하다
* DFS python
def dfs(graph, v, visited):
#visited current node
visited[v] = True
print(v,end=' ')
#visit recursively near visited nodes
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],#number 0 - near nodes' numbers
[2,3,8], #number 1 - near nodes' numbers
[1,7], #number 2
[1,4,5], #number 3
[3,5], #number 4
[3,4], #number 5
[7], #number 6
[2,6,8], #number 7
[1,7] #number 8
]
#visited list
visited = [False]*9
#call dfs function (start from node 1)
dfs(graph,1,visited)
⚡️ ① 그래프를 code로 2차원 리스트로 표현할 수 있고, 위 code와 같이 0번에 인접한 노드 번호, 1번에 인접한 노드 번호들을 각각의 리스트에 담아, 최종 2차원 리스트로 만든다.
⚡️ ② 각 노드가 방문된 정보를 1차원 리스트로 만든다. (default False로 구성)
⚡️ ③ dfs 함수 - 그래프, '첫 출발 노드 번호', 방문 여부 리스트 - 이렇게 세 개를 인자로 넣는 함수를 만든다
→ 재귀함수를 표현해서 현재노드와 연결된 다른 노드를 이중 리스트의 원소로 확인하고, 해당 원소인 노드들의 방문여부가 False라면, 그 노드에 dfs를 더하는 재귀 방식으로 함수를 구현
→ 방문했으면 바로 print
⚡️ 정리) 총 3개 - 그래프 2차원 list + 노드 방문 정보 1차원 list + 첫 출발 node 번호
② BFS(Breadth-First Search)
⚡️ BFS는 너비 우선 탐색이라고도 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘
⚡️ 큐 자료구조를 이용하며, 구체적인 동작 과정은 아래와 같다
(프로그래밍 언어마다 큐 구현 방법을 정확히)
① 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
② 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
(DFS는 인접한 노드 중 방문하지 않은 노드 1개 1개씩 각각 처리를 진행했으나, BFS는 인접한 노드 중 방문하지 않은 모든 노드를 아예 한번에 큐에 넣어 방문 처리하는 차이점!)
③ 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
⚡️ 동작 예시
※ 먼저 방문노드 / 방문기준을 정하는 게 중요
→ 문제마다, 상황마다 방문노드 정하는 기준은 제각각이다
ex) 예시에서는 방문노드는 1, 방문기준은 번호가 낮은 인접노드부터 방문한다고 시작한다.
① [Step 0] 그래프를 준비한다
* 방문기준은 인접한 노드가 여러 개 일때 어떤 노드부터 방문할 지 그 방문기준을 세우는 것을 말한다.
* 간선은 방향이 없는 무방향 간선으로 간주
→ 시작 노드: 1
② [Step 1] 시작 노드인 '1'을 큐에 삽입하고 방문처리를 한다.
③ [Step 2] 큐에서 노드 '1'을 꺼내 방문하지 않은 인접 노드 '2', '3', '8'이 있다.
→ 인접노드 2번, 3번, 8번 노드 모두 큐에 넣고 방문처리 진행
④ [Step 3] 큐에서 노드 '2'를 꺼내 '2'에 방문하지 않은 인접 노드 '7'이 있다.
→ 따라서 7번 노드 큐에 넣고 방문 처리 진행
⑤ [Step 4] 큐에서 노드 '3'을 꺼내 '3'에 방문하지 않은 인접 노드 '4', '5'가 있다.
→ 이 중 4번, 5번 노드 모두 큐에 넣고 방문 처리 진행
⑥ [Step 5] 큐에서 노드 '8'을 꺼냈지만 '8'에 방문하지 않은 인접 노드가 없으므로 무시







⑦ [Step 6] 이러한 과정을 반복하여 전체 노드의 탐색 순서(큐에 들어간 순서)는 아래와 같다.
≫ 탐색순서: 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6
※ 탐색 방향을 구체적으로 돌아보면
▶ 1에서 인접한 방문하지 않은 노드 2 → 3 → 8 방문처리 했다가
▶ 2에서 인접 방문하지 않은 노드 7 방문처리
▶ 그 다음 3을 꺼내 3에서 인접하지 않은 방문 노드 4 → 5 방문처리
▶ 8에서는 인접 방문하지 않은 노드가 없으므로 꺼내기만 함
▶ 그 다음 7을 꺼내 인접하지 않은 방문 노드 6 방문 처리
▶ 모든 노드가 방문 처리되었으므로 끝!
▶ 정리) 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6
▶ 이렇게 시작 노드 1로부터 거리가 가까운 순서대로 방문 처리되고, 거리가 가장 먼 노드가 제일 나중에 방문 처리
→ 각 간선의 비용이 동일한 상황에서 최단 거리로 정말 많이 사용되는 유형(앞선 DFS 유형보다도 실제 움직이는 거리가 적다는 점) 추후 포스팅 참고
* BFS python
from collections import deque
def bfs(graph, start, visited):
queue = deque([start]) #insert start node in queue
visited[start] = True #visited start node
#until queue is empty
while queue:
#pop one node in queue
v = queue.popleft()
print(v,end=' ')
for i in graph[v]:
if not visited[i]:
queue.append(i) #insert all nearest nodes where not visited
visited[i]=True
#2-dimensional graph
graph = [
[],
[2,3,8], #nearest nodes near node 1
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
#visited list
visited = [False] * 9
bfs(graph, 1, visited) #1 2 3 8 7 4 5 6
⚡️ ① DFS와 마찬가지로 그래프, visited 1차원 list, 시작 노드 세 개 준비
⚡️ ② queue에 처음으로 시작 node 넣은 뒤, 재귀가 아니라 queue가 다 빌 때까지 계속 반복 (queue에는 방문한 node만 삽입)
⚡️ ③ queue에 한 개씩 뽑으면서 뽑은 결과 주변 방문 안 한 node queue에 넣고 방문 처리
★ BFS 정리하면 ★ (4개만 정확히 기억하면 끝남)
(1) queue에 start node 넣기, start node 방문 처리
(2) while queue 돌리기
(3) queue.popleft()로 node 한 개 빼기
(4) 한 개 뺀 node의 인접 node for문 돌리기 - 방문 안한 node라면 방문 처리 / queue에 넣기
* DFS / BFS 대표 유형 문제풀이>
Q1. 음료수 얼려 먹기
Q. N X M 크기의 얼음 틀이 있습니다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시됩니다. 구멍이 뚫려 있는 부분까지 상, 하, 좌, 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주합니다. 이 때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하세요. 다음의 4 x 5 얼음 틀 예시에서는 아이스크림이 총 3개 생성됩니다.



A. 전형적인 graph 문제.
⚡️ 문제 해결 아이디어
※ 0으로 연결된 부분을 쭉 깊게 탐색 - DFS로 0 묶음 개수 아이스크림 개수 출력
① 모든 노드에 대하여 각각 0이면 1로 처리한 뒤, 음료수로 먹을 수 있으므로 카운트
② 그 다음 상/하/좌/우로 DFS를 깊게 탐색하며 연결된 부분 모두 0이면 1로 처리 (이미 카운트 1번 했으므로 1로만 모두 처리)
def dfs(x,y):
if x<=-1 or x>=N or y<=-1 or y>=M:
return False
if graph[x][y] == 0:
graph[x][y] = 1
dfs(x-1,y)
dfs(x,y-1)
dfs(x+1,y)
dfs(x,y+1)
return True
return False
N,M=map(int,input().split())
graph=[]
for i in range(N):
graph.append(list(map(int,input())))
result=0
for i in range(N):
for j in range(M):
if dfs(i,j)==True:
result+=1
print(result)Q2. 미로 탈출
Q. N X M 크기의 직사각형 형태의 미로에 갇혔습니다. 미로에는 여러 마리의 괴물이 있어 이를 피해 탈출해야 합니다. 강아지의 위치는 (1,1)이며 미로의 출구는 (N,M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있습니다. 이 때 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있습니다. 미로는 반드시 탈출할 수 있는 형태로 제시됩니다. 이 때 강아지가 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하세요. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산합니다.

A. 출발지 - 목적지가 정해진 경로에서 최단 거리를 구하는 문제
⚡️ 문제 해결 아이디어
※ 매 번 경로 노드를 진행할 때 마다 최단 경로 값을 노드에 저장하며 업데이트 하는 방식
① 처음 (1,1) 위치에서 시작
② 그 다음 BFS로 진행하는 노드마다 최단 경로의 값으로 노드 값을 바꿈
③ 맨 마지막 노드의 값을 출력하면 끝



⚡️ 최단 경로 문제는 무조건 BFS! DFS는 깊이 우선이므로, 모든 경로 각각 감안한 상태로 탐색이 아닌, 한 경로만 먼저 깊게 탐색하므로 최단 경로를 찾기에는 매우 어렵다. 한 번에 전체적으로 탐색해 모든 경로를 감안해 탐색하는 BFS를 <최단 경로> 문제 유형에서는 반드시! 사용하도록 하자
def bfs(x,y):
queue=deque()
queue.append((x,y))
while queue:
x,y=queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx<0 or nx>=n or ny<0 or ny>=m:
continue
if graph[nx][ny] == 0:
continue
if graph[nx][ny]==1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx,ny))
return graph[n-1][m-1]
from collections import deque
n,m=map(int,input().split())
graph=[]
for i in range(n):
graph.append(list(map(int,input())))
dx=[-1,1,0,0]
dy=[0,0,-1,1]
print(bfs(0,0))- 이코테 2021 출처 -
'Computer Science > Algorithms' 카테고리의 다른 글
| 👀 Binary Search 👀 (2) | 2022.12.06 |
|---|---|
| understanding pesudo-code of QuickSort (0) | 2022.12.05 |
| 🧭Recursion (0) | 2022.09.27 |
| Implementation (1) | 2022.09.21 |
| Greedy (0) | 2022.09.12 |


댓글