1. 개요
→ 모수 θ의 추정에 사용되는 통계량을 θ의 추정량(θhat으로 표기)이라고 함
→ 추정을 목적으로 하는 표본통계량
모수(θ) 👉 추정량(=표본통계량; θhat) - 추정치(관찰값)
Q) 그렇다면 모수를 추정하는 방법은?
1> 점추정(point estimation)
= 하나의 모수를 '한 개의 값'으로 추정
2> 구간추정(interval estimation)
= '모수가 포함되리라 기대되는 구간으로 모수 추정' (점추정을 보완한 것)
※ 점 추정은 표본정보를 하나의 값으로 요약하여 모수를 추정하지만, 구간 추정은 모수가 포함될 것으로 예상되는 구간을 이용하여 모수 추정
→ 점추정을 하면 얼마만큼의 신뢰도로 해당 모수를 추정해서 맞힐 수 있는 지 모르기에 구간추정을 통해 점추정의 한계를 보완
2. 신뢰구간
* statistical test를 시각적으로 표현할 수 있다는 점에서 정말 유용하게 쓰일 수 있는 게 신뢰구간!
[1] 정의
"구간추정을 위한 모수 θ에의 신뢰구간"
* 신뢰구간 도출을 위해 알아야 하는 것
1> 추정량 θhat
2> 추정량 θhat의 표본분포
* 정의
→ 추정량 θhat을 적절하게 변형한 L과 U가 있고 만약
P[L <= θ <= U] = 1 - α (0<= α <= 1)
와 같다면 구간 (L,U)를 '모수 θ의 100(1-α)% 신뢰구간'이라 한다
→ 100(1-α)%: 신뢰수준 (여기서 α는 매우 작은 수준)
→ 신뢰수준이 높을수록 해당 구간이 모수를 포함할 가능성이 높음
[2] '모평균 μ'에 관한 신뢰구간
✌️ 그러면 이제 모수를 모평균μ라고 하고, 모평균μ에 관한 신뢰구간을 구해보자
🤞 모수를 위한 추정량 θhat은 표본평균 x̄로 해당 표본평균의 표본분포까지 알아야 한다
([1]에서 신뢰구간 도출을 위해 추정량과 추정량의 표본분포까지 알아야 한다고 했음!)
> 추정량의 표본분포 <
→ 모집단이 정규분포를 따라야 하고 ①
→ 모집단의 모분산이 알려져야 하는 가정을 따른다 ② (드문 케이스)
→ 즉! X1 ~ Xn이 정규모집단(모분산이 알려진)으로부터의 확률표본이라 하고 x̄ 표본평균의 분포는 N[μ, (모분산)^2/n]를 따른다
(관련 포스팅 아래 참조)
<추정과 검정> - 추론 개요
1. 통계적 추론 개요 [1] 관련 기본 개념 → 모집단 = 관심대상을 다 모아 둔 것 → 모수 = 해당 모집단(↑)을 대표하는 값. 모집단의 특징을 요약하는 '수' (예를 들면 모집단의 평균, 분산) "but 우
sh-avid-learner.tistory.com
→ 이를 좀 더 쉽게 Z에 관해서 나타낸다면
- Z분포 및 3가지로 표현되는 동일한 의미의 신뢰구간 -
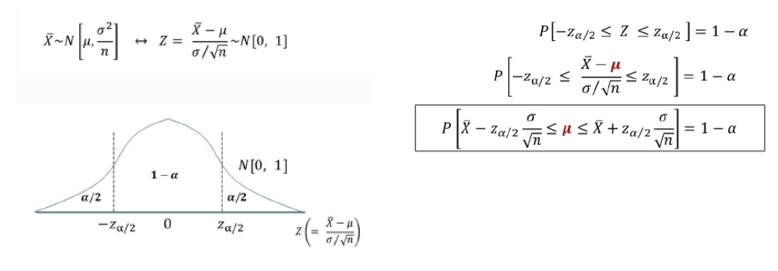
- 여기서 Z는 표준 정규분포를 따르며, 관심있는 신뢰수준을 분포 그래프의 가운데에 둘 수 있다 (위 그림과 같이)
- Z=0을 기준으로 좌우대칭인 분포
[3] 신뢰구간 해석
"동일한 구간 추정법을 반복적으로 사용할 때 얻어지는 신뢰구간들이 참값(모수) θ를 품을 확률"
"이 한 개의 신뢰구간이 모수를 포함할 확률"
→ 신뢰도가 정해지면 이 신뢰구간의 길이는 정해짐, 표본평균이 달라지기에 구간의 위치는 계속 바뀜!
→ 이 때 위치가 바뀌는 여러 신뢰구간들 중 모수를 포함한 신뢰구간의 개수(이것이 신뢰도! - 아래 그림 확인)를 뜻함
(n개의 표본으로 구한 하나의 신뢰구간에 모수가 포함되는 지의 여부는 알 수 없다는 뜻임!)
- 95% 신뢰도 - 총 20개 중 1개의 신뢰구간만 모수를 포함 x -

🙌 추가적으로 두 means 비교를 위해 independent two-samples t-tests를 거치지 않고도, 두 신뢰구간이 overlap되지 않는다면 statistically significant difference (between two means)를 보일 수 있다! (그만큼 시각적으로 강력한 '신뢰구간'!)
☆ 단, overlap 된다면 실제 t-test를 거쳐서 자세하게 확인해봐야 함
[4] 신뢰구간의 오차한계
"👐 '신뢰수준이 👆 & 오차한계 👇 수록 좋은 신뢰구간'"
* 오차한계 - margin of error = '신뢰구간 길이의 절반'
- 초록색이 오차한계 -
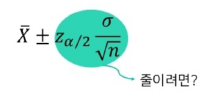
→ 오차한계를 줄이려면? (1) 표본 수 n 키우기 or (2) 신뢰수준 낮추기
* 신뢰수준 & 오차한계는 상충관계
- 신뢰수준을 높이려면 구간이 길어져 오차한계가 커짐
- 따라서 반대로 구간의 길이를 줄이려 하면 신뢰수준이 낮아짐
3. 예제 + 코드 구현
Q) '어떤 수산물 상점에서 판매하는 고등어의 체장을 파악하고자 7마리를 추출하여 그 체장을 조사. 다음 7개의 체장 data를 수집함 (28.9, 32.4, 29.8, 30.6, 27.8, 29.4, 31.3). 고등어의 체장은 정규분포를 따르며 고등어 체장의 표준편차가 1.5로 알려져 있다고 할 때 (모집단 정규분포 & 모분산 두 가지 가정 모두 만족), 90%의 신뢰수준에서 고등어 체장의 신뢰구간은?
정리> 우리는 주어진 7개의 sample data를 통해 전체 고등어 모집단의 체장 평균을 알아보려 한다! 신뢰도를 사용하여 신뢰구간을 구해보자
A1) (using concepts)
- 표본평균 x̄ (7개로 뽑은 표본들의 평균) = 30.029
- Z = 신뢰수준 90%에 따른 Z는 표를 따로 참고하면 1.645값이다
- 모표준편차σ = 1.5로 알려짐
- 표본의 크기n = 7
→ 신뢰구간을 나타내면
- 90% 신뢰구간 -

∴ 즉, 위에 제시된 90%신뢰구간에 고등어 체장의 모집단 평균이 포함될 확률은 90%로 신뢰할 수 있다.
👍 다시 말하면? 전체 고등어집단의 체장평균이 29.096 이상이고 30.962이하일 확률이 90%이다! 끝! 완벽정리 완료! 👍
A2) (using python code)
* 너무 친절하시게도 scipy library에서 confidence interval(신뢰구간)을 출력해주는 method를 제공해준다..!
(주의 - 모집단 data - 즉 고등어 체장 data 수가 30개가 넘고 정규분포를 만족한다 가정한다 - scipy.stats.norm 사용)
(만약에 모집단 data가 30보다 작은 소규모였다면 normal-distribution이 아닌 t-distribution 활용 - 추후 t분포 포스팅 참고!)
¶ scipy.stats.norm docu ¶
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html
▶ norm의 interval method 활용 ◀
- alpha는 신뢰도, loc은 신뢰구간의 중심, scale은 오차한계에서 Z값을 나눈 값 -

import numpy as np
from scipy.stats import norm
sample = [28.9, 32.4, 29.8, 30.6, 27.8, 29.4, 31.3]
CI = norm.interval(alpha = 0.9, loc = np.mean(sample), scale = 1.5/np.sqrt(len(sample)))
CI #Z값 1.6448536269
*** 최종 CI 출력 결과 ***
(29.09602707713939, 30.961115780003475)
👍 다시 말하면? 전체 고등어집단의 체장평균이 29.09602707713939 이상이고 30.961115780003475 이하일 확률이 90%이다! 끝! 완벽정리 완료! 👍
Q. 위 A1과 값이 좀 차이나는 이유?
1> A1의 경우 눈대중으로 어림잡아 Z값을 정했다.
- 표에 의해 1.64와 1.65 어딘가 중간쯤...? 그래서 어림잡아 1.645로 정했어서 -

2> 평균을 소수점 셋째자리까지 자름...!
> scipy로 한 결과가 더 정확하고 scipy 결과로 나온 신뢰구간을 바탕으로 역으로 계산해보면 Z값은 1.64485쯤 정도 나온다
* 표출처) https://math100.tistory.com/53
* 썸네일출처) https://www.simplypsychology.org/confidence-interval.html
- 내용 출처 - 공공데이터 청년인턴(일경험수련생) 상시 교육 ProDS 데이터분석이론 (초급+중급)1
'Statistics > Concepts(+codes)' 카테고리의 다른 글
| T-test 👉《Two-samples 'independent' T-test (w/python code)》 (0) | 2022.04.20 |
|---|---|
| descriptive statistics & inferential statistics (0) | 2022.04.15 |
| T-test 👉 《One-sample T-test (w/ python code)》 (0) | 2022.04.05 |
| <추정과 검정> - 표본추출법 (w/ python code) (2/2) (0) | 2022.03.30 |
| <추정과 검정> - 표본추출법 (w/ python code) (1/2) (0) | 2022.03.25 |


댓글