** ML 모델의 성능을 최종적으로 평가할 때 다양한 evaluation metrics를 사용할 수 있다고 했음! **
(supervised learning - regression problem에서 많이 쓰이는 평가지표들)
- 과정 (5) -

😙 그러면 차근차근! 각 평가지표에 대해서 자세히 알아보려고 함! 😙
- ①MSE ②MAE ③RMSE ④R-Squared -
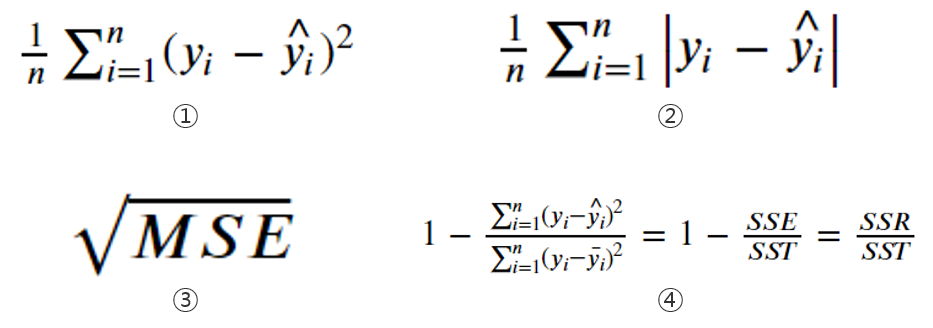
1. MSE(Mean-Squared Error)
🤔 linear regression model concept에 대해서 배울 때 관측치와 예측치의 차이들의 합인 SSE를 최소로 하는 'least squares method'를 기반으로 선형회귀모델을 결정한다고 배웠다
≫ 이 SSE를 전체 데이터 개수 n으로 나눈 값, 즉 '관측치와 예측치의 차이들'의 평균을 우리는 'MSE(Mean-Squared Error)'라고 부름.
→ 매우 많이 쓰는 evaluation metric!
→ 하지만 제곱을 하는 metric이기에 단위 scale 변화 폭이 커서 오류 확인 시 어느 정도 크기의 오류인 지 알아보기가 어려운 단점이 있음
→ 즉, 이상치가 존재한다면 제곱으로 인해 더 튀어 보여! 이상치에 민감하다는 단점을 갖고 있다고 말할 수 있다
'This metric displays plausible magnitude of error term, If we try to say it in another way, it is the standard deviation of prediction error or Residuals(it shows large number of deviations well). Obviously this measure shows us how data concentrated around the best fit line in a regression problem.'
→ 실제 값으로부터 어느 정도 떨어져 있는 지 알 수 있는 수치로 - 바꿔 말하자면 만들어진 model로부터 data가 어느 정도 거리에 집중되어 있는 지 알 수 있는 지표이다
2. MAE(Mean-Absolute Error)
≫ MSE와 다르게 MAE는 단위 scale이 변하지 않게 '관측치와 예측치의 차이 절댓값(즉 차이 크기 그 자체)'의 평균을 우리는 'MAE(Mean-Absolute Error)'라고 부른다!
→ 즉, 오류가 났을 때 scale의 변화 고려 없이 오류 자체를 바로 확인이 가능하다는 점!
→ 직관적으로 이상치에 큰 영향을 받지 않는다
'MAE doesn’t consider direction of data and also is linear score, means that all the individual errors (vertical lines) are weighted equally in the average.'
→ error 크기 그 자체가 평가수치로 반영되기 때문에 모든 error가 가중치가 없이 그대로 간주된다! (MSE에 비해 이상치 영향 미미)
3. RMSE(Root Mean-Squared Error)
≫ 제곱으로 인해 MSE가 스케일 변화 폭이 크고 이상치에 민감한 반응을 보여 이를 줄이기 위해 MSE에 root를 씌운 값이 RMSE!
→ 하지만 제곱의 합을 root로 씌웠다고 해서 정확히 차이 크기 자체만으로 평가한 MAE에 비해서는 평가수치를 구하는 식을 따졌을 때 이상치에 민감할 수 밖에 없다
→ root를 씌웠으니 MAE와 비슷한게 아닌가 싶기도 하지만 MAE와 RMSE는 명백한 차이가 존재
따라서..
<RMSE & MAE를 비교해보면.. 😉>
'RMSE and MAE both focused on prediction errors and both don’t consider the direction of errors. However there are some differences between them; the most significant difference is that RMSE in the first step takes square of residuals then takes average of them it means that it assigns more weight to bigger prediction errors although MAE considers identical weight for all residuals; so we can see RMSE demonstrates the standard deviation of prediction errors, in other words RMSE has direct correlation with the variance of frequency distribution of errors.'
→ MAE는 모든 error의 가중치가 동일하다 & 하지만 RMSE의 경우 크기가 더 큰 error에 가중치를 더 둔다
→ 이는 다르게 어떻게 해석할 수 있냐면, RMSE는 예측 error의 표준편차를 나타낸다고 할 수 있다. 즉 큰 error가 있다면 그에 가중치를 두어 RMSE가 커진다는 건 = 기존 분포에서 벗어난 data가 존재해 흩어져 있다는 뜻으로 표준편차가 크다라고 말할 수 있다('RMSE is sensitive to error distribution of sample'). 따라서 MAE와 달리 RMSE를 통해 우리는 유달리 기존 model에서 벗어나게 예측된 이상치스러운(?) error들이 있냐를 MAE 수치보다는 더 직관적이고 쉽게 알 수가 있는 것이다 👍
→ 예를 들어 보자면,,

- 첫 행의 경우 MAE와 RMSE의 차이가 0.02밖에 나질 않는다
- 하지만 두 번째 행의 경우 MAE에 비해 RMSE가 0.27이나 크다 (첫 행보단 월등치 차이나는 수치). 그 이유는 두 번째 행에 보면 3이라는 actual value를 1로 예측해서 error가 2인데 반해, 첫 행의 경우 error가 0.2밖에 안난다. error 크기가 큰 값에 더 weight가 부과되어 결과론적으로 RMSE 수치가 큰 차이가 나게 만든 것이다
→ 실제 실용적으로 RMSE는 제곱이라는 계산이 들어가서 gradient descent를 계산할 때 미분 편의를 위해 MAE보다 더 선호하는 metrics이고 (gradient descent 관련 내용 추후 포스팅) & MAE는 모델 간의 직접적인 비교를 할 때 한 번에 직관적으로 알 수 있으므로 RMSE보다 더 선호하는 편이다.
4. R-squared
≫ 약간 복잡 ≪
→ 회귀모델의 설명력을 표현하는 지표. 정확성을 나타내는 일종의 SCORE
→ 0과 1사이의 지표로 나타냄. 1에 가까울수록 좋음
→ 얼마나 회귀모델 regression line이 실제 값을 예측하는 지 평가하는 지표
→ 식을 구할 때 평균 개념이 들어감
<< SST = SSE + SSR >>
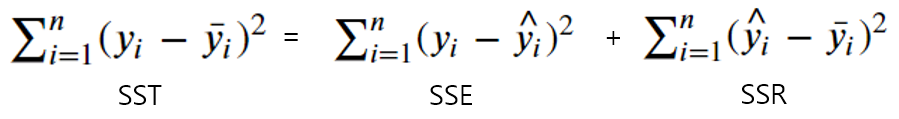
⊃ SSE(Sum of Squared Error)= 위에서 언급한 least squares method에서 사용한, 실제값과 예측값의 차이를 제곱한 값들의 합!
⊃ SSR(Sum of Squared due to Regression - regression model에서의 값을 평균 개념을 사용해 수치로 표현) = 실제값이 아니라 실제값들의 평균과 예측값의 차이를 제곱한 값들의 합!
⊃ SST(Sum of Squares Total) = 실제값들의 평균과 실제값의 차이를 제곱한 값들의 합!
→ R-squared는 SSR/SST로 SSR을 SST로 나눈 값을 뜻한다
→ 즉, 실제값에 비해 예측값이 얼마나 실제값에 가까운 지 나타내는 지표로, 1에 가까울수록 goodness of fit(fitting의 정확성)이 크다고 말할 수 있음 ㅇㅇ
- 즉 아래처럼 표현도 가능 -

※ R-squared 값이 0이면 SSR이 0임을 뜻하므로 SST = SSE, 즉 실제 target값들의 평균값만 가지는 일종의 직선 모델 (baseline model)임을 뜻함. (추가 평가지표들과 함께 다시 비교 & 정리한 글 추후 포스팅)
→ 위에서 언급한 세 수치 MSE, MAE, RMSE는 error 그 자체에 초점을 두었다면 R^2는 얼마나 model을 잘 설명하였는 가를 설명하는 척도로 일종의 '설명력', '점수' 차원으로 말할 수 있음 👱
w/ scikit-learn
→ sklearn.metrics module에 이미 함수로 내장되어 있다. 그대로 갖다 쓰기만 하면 됨
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
→ 모두 인자에 y_true & y_pred 집어넣으면 바로 계산할 수 있다 (RMSE는 mean_squared_error 구한 값에 root 씌우기)
→ 여기서 y_true는 실제 관측치 data / y_pred는 regression line 위의 data로 둘 다 각각 배열 형태로 집어넣는다
* 출처) https://towardsdatascience.com/art-of-choosing-metrics-in-supervised-models-part-1-f960ae46902e
'Machine Learning > Fundamentals' 카테고리의 다른 글
| One-Hot encoding (0) | 2022.04.17 |
|---|---|
| Cross-Validation (concepts + w/code) (0) | 2022.04.17 |
| Overfitting/Underfitting & Bias/Variance Tradeoff (0) | 2022.04.17 |
| intro. Machine Learning (0) | 2022.04.15 |
| Baseline Model (0) | 2022.04.13 |


댓글