** 우리는 저번 포스팅에서 Supervised Learning 중 Regression의 일종인 'linear regression'에 대해 학습했다.

☝️ 위 그림에서 보다시피 linear 선형 regression으로는 많은 종류의 model이 있음을 확인할 수 있다
🔆 우리는 이 선형회귀모델 중 대표적인 'Ridge 릿지 회귀'에 대해서 이번 포스팅을 통해 알아보려 한다!
starting from Overfitting...
👏 기존 단순선형/다중선형 회귀선이 과적합이 일어날 가능성이 있어서 일반화가 잘되는 (즉, variance를 낮추는 방향) 쪽으로 tuning하는 modelling 방법이다! 👏
(↓ovefitting / underfitting 관련 개념은 아래 posting 참조)
Overfitting/Underfitting & Bias/Variance Tradeoff
1. 일반화(generalization) "In machine learning, generalization is a definition to demonstrate how well is a trained model to classify or forecast unseen data. Training a generalized machine learnin..
sh-avid-learner.tistory.com
- 그림으로 모두 설명이 되는 릿지! -

→ 👍 위 그림에서처럼 ①the sum of the squared residuals(SSR)과 ②lambda*(the sum of (slope)^2)의 합 (곧 cost function)이 최소화가 되는 직선이 곧 ridge regression model이다! (즉 1)SSR + 2)회귀계수제곱합을 최소화하기)
→ n은 샘플 수, p는 특성 수, λ는 tuning parameter(alpha = lambda = regularization parameter = penalty term) - penalty 심각정도
Q. 간단한 예 살펴보기

- 순서대로 기억 (위 그림)-
1> 기존에 빨간 점에 100% 과적합되어 있던 단순선형회귀 빨간 선이 있다
2> 과적합의 문제로 인해 새롭게 입력된 연두색 값들에 대한 예측 정확성이 매우매우 떨어짐!
3> 따라서 우리는 해당 회귀선에 penalty((계수제곱합*λ))를 부과해 기울기를 점점 조금씩 낮춰 위 cost function으로 정의한 1)과 2)의 합이 최소가 될 때를 찾는다!
4> 찾으면 그 때의 직선이 곧 우리가 찾은 Ridge Regression Model
즉.. 'by starting with a slightly worse fit, Ridge Regression can provide better long term predictions'
small amount of Bias가 발생하지만..! 👉 significant drop in Variance의 효과 매우 Good
🗣 여기서 λ는?
<<λ는 0이상의 실수 값을 가지며 λ를 높인다는 건 cost function 측면에서 cost function 값을 최소화해야하므로 같이 곱해지는 항인 회귀계수제곱합을 더 줄여야 한다 - 따라서 λ를 높인다는 건 회귀계수(coefficeints)의 효과를(magnitude) 더 줄인다고 말할 수 있음)>>
→ 위에서 언급했다 싶이 lamba를 통해 우리는 다중공선성의 문제를 발생시킬 수 있는 (변수들 간의 영향 받음) 문제를 줄일 수 있다. (penalty를 부과해서 변수 중요도를 낮추므로!)
(즉, slope 회귀계수 기울기 값이 감소한다는 건 예측값y가 다른 축들의 변화에 따라 덜 민감해진다는 뜻이 된다)
→ 이렇게 편향을 조금 더하고 & 분산을 줄이는 방법을 정규화(Regularization - 엄밀히 말하면 L2 Regularization)이라고 한다!
(추후 regularization & standardization & normalization 차이 포스팅)
(추후 L1 Regularization을 통해 구하는 Lasso까지 비교하며 차이 포스팅)
→ 그럼 최적의 λ값을 구하는 방법은? CV(cross-validation)을 사용해서 parameter tuning을 통해 찾아야 한다
(다음에 배울 내장함수에 이미 다 들어 있음)
Cross-Validation (concepts)
* 머신러닝을 위해서 무.조.건. 알아야 하는 CROSS-VALIDATION! 간단히 개념만 알아보ZA * - 2번 과정 - model selection에서 주로 많이 쓰이는 cross-validation 기법 - 🧐 PURPOSE? 'The purpose of cross..
sh-avid-learner.tistory.com
"ridge의 역할: λ를 통해 shrinking coefficients 효과 - MSE 줄이기"
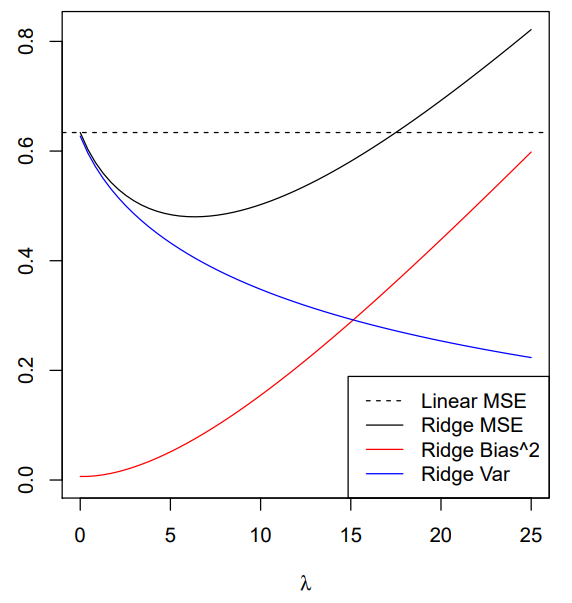
🖐 위 그림에서 볼 수 있듯이 penalty에 따른 Bias-Variance tradeoff 관계를 잘 보여주고 있다. 어느 정도 규제를 가하면 ridge로 인해 해당 모델의 MSE값이 감소하여 좋은 성능을 보이나 너무 심하게 규제를 가할수록 Bias로 인해 MSE값이 다시 커지는 걸(오히려 기존 Linear Regression model보다도 더 안좋은 성능을 보인다) 확인할 수 있다.
→ 즉, 적절한 규제가 가했을 때에 멈추는 것이 최상의 시나리오
Q. 기존 coefficients의 크기에 따라 Ridge 성능 개선에 차이가 있을까?
A. 있다.
"Ridge regression performs particularly well when there is a subset of true coefficients that are small or even zero. It doesn’t do as well when all of the true coefficients are moderately large; however, in this case it can still outperform linear regression over a pretty narrow range of (small) λ values"
→ 기존 term들의 계수가 작을 때 ridge의 효과가 더 빛을 발한다. 하지만 그렇다고 해서 계수가 클 때 성능 개선이 없는 건 아니다(기존 linear regression보다 성능 개선이 있긴 있다!). 다만 더 드라마틱한 성능 개선은 coefficients가 상대적으로 작을 때 볼 수 있다.
- 이후 실험을 통해 증명해보자! -
* for discrete variables>
→ 위에서 언급한 case는 independent variable이 continuous할 경우이다. 그렇다면 discrete이면 어떻게 연산될까?
→ ex) normal diet, high-fat diet 두 가지 discrete variable이 있다고 가정하자

- 여기서 우리는 식을 size = a + b x (high-fat diet)라 세운다. a는 normal diet의 평균 mean, b는 normal diet의 평균과 high-fat diet 평균의 차이를 의미한다.
- high-fat diet 값이 0인 경우 계수 a 자체로 normal diet를 예측하며, high-fat diet값이 1인 경우 a+b 두 계수의 합이 high-fat diet를 예측한다.
- ridge 모델을 통해 SSR(Sum of Squared Residuals - 각 variable 실제 값과 각 variable 별 평균의 차이 제곱합) + $\lambda$x$b^2$을 줄여야 한다.
- 만약에 $\lambda$를 높인다면? = 반대로 b를 줄여야 하므로, 두 variable의 평균 차이가 줄어든다. 즉, 이 뜻은 위 그림의 경우 high-fat-diet가 두 variable 평균 차이에 더 무감각해진다는 뜻.
→ 즉 우리는 penalty인 $\lambda$를 높이면서 두 discrete variable의 mean 차이를 줄여 주어진 data에 과적합되지 않은 ridge model을 구축한다.
** 출처 https://www.youtube.com/watch?v=Q81RR3yKn30 (PARTY MORE STUDY LESS by StatQuest~ 🙆🏼)
** 출처 https://www.mygreatlearning.com/blog/what-is-ridge-regression/
** 출처 https://www.stat.cmu.edu/~ryantibs/datamining/lectures/16-modr1.pdf
'Machine Learning > Models (with codes)' 카테고리의 다른 글
| Logistic Regression Model (concepts) (0) | 2022.04.24 |
|---|---|
| (L2 Regularization) → Ridge Regression (w/scikit-learn) (0) | 2022.04.20 |
| Multiple Linear Regression Model (concepts+w/code) (0) | 2022.04.17 |
| Simple Linear Regression Model (w/scikit-learn) (0) | 2022.04.16 |
| Simple Linear Regression (concepts) (0) | 2022.04.14 |


댓글