MLE for the normal distribution

🔊 저번 시간에 MLE에 대해서 배웠다. 그리고 예제로 MLE 기법을 logistic regression에 적용해 최적의 sigmoid 함수를 어떻게 구하는 지 수학적으로 수식을 통해 알아보았다.

 

🔊 이번 시간에는 logistic이 아닌 normal distribution에 MLE 기법을 적용해 주어진 data를 가장 잘 설명하는 normal distribution의 두 모수인 μ와 σ를 찾아 최적의 normal distribution을 알아보는 시간을 가져보려 한다.

 

Maximum Likelihood Estimation(MLE)

* normal distribution 개요>

pr(x|μ,σ) = 1σ√2π e−12(x−μσ)2

 

 

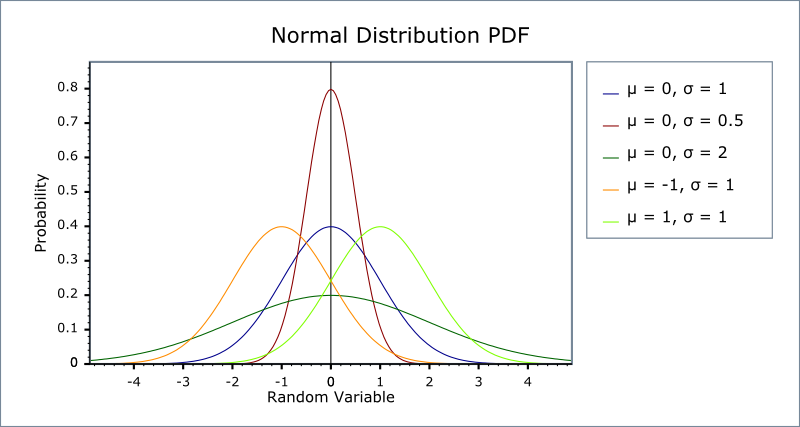
→ 위 그림에서 보듯이 distribution의 이동 방향은 μ가 결정해준다. 분포 전체의 평균인 중심을 뜻한다. μ 값이 크면 오른쪽으로 이동, 작으면 왼쪽으로 이동한다.

→ distribution의 너비, 즉 양 옆으로 퍼진 정도는 σ가 결정해준다. σ 값이 클수록 양 옆으로 퍼지고, 작을수록 위로 뾰족해진다.

 

🌿 우리는 해당 distribution 함수를 likelihood로 두어 해당 likelihood가 최대가 될 때의 distribution을 찾으려 한다 (두 모수 찾기)

 

🌿 L(μ,σ|x) = 1σ√2π e−12(x−μσ)2

 

🌿 speculation) 주어진 x data들이 있을 때, 해당 x data들을 가장 잘 설명하는 normal distribution은 주어진 x data의 평균이 해당 distribution의 모수 μ이고, 주어진 x data의 표준편차가 distribution의 σ라고 추측할 수 있다.

 

🌿 MLE 기법으로 증명해보자.

* using MLE>

※ 주의 - 모수가 2개 이상인 경우 각 모수별로 편미분할 때, 다른 모수는 constant 취급한 채로 편미분

 

① 전체 likelihood는 각 x point별 likelihood를 모두 곱한 값이다

→ L(μ,σ|x1,x2,...,xn) = L(μ,σ|x1) x L(μ,σ|xn) = 1σ√2π x e−12(x1−μσ)2 x ... x 1σ√2π x e−12(xn−μσ)2

 

② 미분연산 편의를 위해 양변에 ln 로그를 취하면

→ ln[L(μ,σ|x1,x2,...,xn)] = ln(1σ√2π x e−12(x1−μσ)2 x ... x 1σ√2π x e−12(xn−μσ)2)

 

③ 우변 ln을 쭉 풀고 계산하면

→ = ln(1σ√2π x e−12(x1−μσ)2) + ... + ln(1σ√2π x e−12(xn−μσ)2)

= ln[(2πσ2)−1/2] - (x1−μ)22σ2ln(e) + ... + ln[(2πσ2)−1/2] - (xn−μ)22σ2ln(e)

= -12ln(2πσ2) - (x1−μ)22σ2 + ... + -12ln(2πσ2) - (xn−μ)22σ2

= -12ln(2π) -12ln(σ2) - (x1−μ)22σ2 + ... + -12ln(2π) -12ln(σ2) - (xn−μ)22σ2

= -12ln(2π) -ln(σ) - (x1−μ)22σ2 + ... + -12ln(2π) -ln(σ) - (xn−μ)22σ2

 

④ 공통된 항들을 묶어 표현하면 ln 연산을 간단하게 완성할 수 있다.

→ = -n2ln(2π) -nln(σ) - (x1−μ)22σ2 - ... - (xn−μ)22σ2

 

⑤ (1) 이제 μ에 관한 편미분을 해보면

→ ∂∂μ ln[L(μ,σ|x1,x2,...,xn)] = 0 - 0 + x1−μσ2 + ... + xn−μσ2

= 1σ2 [(x1+...+xn)−nμ]

 

⑥ (2) σ에 관한 편미분을 해보면

→ ∂∂σ ln[L(μ,σ|x1,x2,...,xn)] = 0 -nσ + (x1−μ)2σ3 + ... + (xn−μ)2σ3 = -nσ + 1σ3[(x1−μ)2+...+(xn−μ)2]

 

⑦ 두 모수에의 편미분 값이 0일 때를 확인 (최대치이므로)

→ 1> 0 = 1σ2 [(x1+...+xn)−nμ]

↔ 0 = (x1+...xn)−nμ

↔ μ = (x1+...xn)n

 

→ 2> 0 = -nσ + 1σ3[(x1−μ)2+...+(xn−μ)2]

↔ 0 = −n + 1σ2[(x1−μ)2+...+(xn−μ)2]

↔ σ = √(x1−μ)2+...+(xn−μ)2n

 

⑧ 결과, 최적의 μ는 주어진 data의 평균, 최적의 σ는 주어진 data의 표준편차임을 MLE 기법을 통해 증명하였다! 

(위의 speculation이 맞았음 확인 가능)

---

* 출처) 갓 STATQUEST https://www.youtube.com/watch?v=Dn6b9fCIUpM 

* 사진, 썸넬출처) https://www.boost.org/doc/libs/1_49_0/libs/math/doc/sf_and_dist/graphs/normal_pdf.png